题目内容
 (2013•双峰县模拟)如图,为了宣示钓鱼岛主权,中国政府派飞机对钓鱼岛海域配合海监船进行立体巡防.某飞机在巡防中由西向东经过钓鱼岛的上空,飞机在距海平面垂直高度为100米的点C处测得钓鱼岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得钓鱼岛的东端点B的俯角为45°,求钓鱼岛东西两端BA的距离(结果精确到0.1米,参考数据:
(2013•双峰县模拟)如图,为了宣示钓鱼岛主权,中国政府派飞机对钓鱼岛海域配合海监船进行立体巡防.某飞机在巡防中由西向东经过钓鱼岛的上空,飞机在距海平面垂直高度为100米的点C处测得钓鱼岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得钓鱼岛的东端点B的俯角为45°,求钓鱼岛东西两端BA的距离(结果精确到0.1米,参考数据:| 3 |
| 2 |
分析:首先过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,易得四边形ABFE为矩形,根据矩形的性质,可得AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=3500米,然后分别在Rt△AEC与Rt△BFD中,利用三角函数即可求得CE与DF的长,继而求得岛屿两端A、B的距离.
解答:解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=100米,CD=3500米.
在Rt△AEC中,∠C=60°,AE=100米.
∴CE=
=
=
(米),
在Rt△BFD中,∠BDF=45°,BF=100.
∴DF=BF=100(米).
∴AB=EF=CD+DF-CE=3500+100-
≈3600-
×1.73≈3542.3(米),
答:岛屿两端A.B的距离为3542.3米.

∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=100米,CD=3500米.
在Rt△AEC中,∠C=60°,AE=100米.
∴CE=
| AE |
| tan60° |
| 100 | ||
|
| 100 |
| 3 |
| 3 |
在Rt△BFD中,∠BDF=45°,BF=100.
∴DF=BF=100(米).
∴AB=EF=CD+DF-CE=3500+100-
| 100 |
| 3 |
| 3 |
| 100 |
| 3 |
答:岛屿两端A.B的距离为3542.3米.
点评:此题考查了俯角的定义、解直角三角形与矩形的性质.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
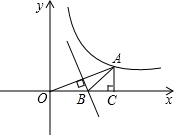 (2013•双峰县模拟)如图,点A(3,n)在双曲线y=
(2013•双峰县模拟)如图,点A(3,n)在双曲线y=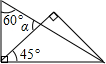 (2013•双峰县模拟)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是
(2013•双峰县模拟)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是