ÌâÄ¿ÄÚÈÝ
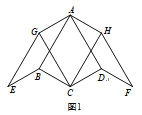
¡ŸÌâÄ¿¡¿ÔÚËıßÐÎ ABCDÖУ¬AB£œAD£¬¡ÏBAD£œ60¡ã£¬±ßBCÈƵãB˳ʱÕëÐýת120¡ãµÃµœBE£¬±ßDCÈƵãDÄæʱÕëÐýת120¡ãµÃµœDF£¬ËıßÐÎABEGºÍËıßÐÎADFHΪƜÐÐËıßÐΣ®
£š1£©ÈçÍŒ1£¬ÈôBC£œCD£¬¡ÏBCD£œ120¡ã£¬Ôò¡ÏGCH£œ_______¡ã£»
£š2£©ÈçÍŒ2£¬ÈôBC¡ÙCD£¬ÌœŸ¿¡ÏGCHµÄŽóСÊÇ·ñ·¢Éú±ä»¯£¬²¢Ö€Ã÷ÄãµÄœáÂÛ£»
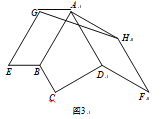
£š3£©ÈçÍŒ3£¬Èô¡ÏBCD£œ¡ÏADC£œ90¡ã£¬AB£œ![]() ÇëÖ±œÓÐŽ³ö¡÷AGHµÄÖܳ€£®
ÇëÖ±œÓÐŽ³ö¡÷AGHµÄÖܳ€£®

¡ŸŽð°ž¡¿£š1£©60£»£š2£©²»±ä£¬ÀíÓÉŒûœâÎö£»£š3£©![]() £®
£®
¡ŸœâÎö¡¿
£š1£©Á¬œÓAC£¬Ö€Ã÷![]()
![]() £¬ŒŽ¿ÉµÃ
£¬ŒŽ¿ÉµÃ![]() £»
£»
£š2£©²»±ä£¬![]() £¬Á¬œÓ
£¬Á¬œÓ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() Óë
Óë![]() œ»ÓÚµã
œ»ÓÚµã![]() £¬ÒòΪ
£¬ÒòΪ![]() £¬
£¬![]() £¬µÃµœ
£¬µÃµœ![]() ΪµÈ±ßÈýœÇÐΣ¬ÓÖÒòΪËıßÐÎ
ΪµÈ±ßÈýœÇÐΣ¬ÓÖÒòΪËıßÐÎ![]() ÊÇÆœÐÐËıßÐΣ¬¿ÉµÃ
ÊÇÆœÐÐËıßÐΣ¬¿ÉµÃ![]() £¬
£¬![]() £¬ÒòΪ
£¬ÒòΪ![]() £¬ËùÒÔ
£¬ËùÒÔ![]() £¬ÒòΪ
£¬ÒòΪ![]() £¬
£¬![]() £¬µÃµœ
£¬µÃµœ![]() £¬ŒŽ
£¬ŒŽ![]() £¬
£¬
¿ÉÖ€![]() £¬µÃµœ
£¬µÃµœ![]() £¬
£¬![]() £¬Í¬Àí¿ÉµÃ£¬
£¬Í¬Àí¿ÉµÃ£¬![]() £¬ µÃ
£¬ µÃ![]() £¬
£¬![]() £¬ÒòΪ
£¬ÒòΪ![]() £¬
£¬![]() £¬
£¬![]() £¬ËùÒÔ
£¬ËùÒÔ![]() £¬ÒòΪ
£¬ÒòΪ![]() £¬
£¬![]() £¬
£¬![]() £¬¿ÉÖ€
£¬¿ÉÖ€![]() £¬¿ÉµÃ
£¬¿ÉµÃ![]() £¬
£¬![]() £¬ÓɵÈÁ¿¹Øϵ¿ÉµÃ
£¬ÓɵÈÁ¿¹Øϵ¿ÉµÃ![]() £»
£»
£š3£©·Ö±ðÇó³öAG¡¢AH¡¢GHµÄ³€£¬Ö±œÓÏàŒÓŒŽ¿É£»
œâ£º£š1£©ÈçÍŒ£¬Á¬œÓAC£¬
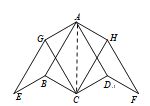
ÔÚ![]() ºÍ
ºÍ![]() ÖУ¬
ÖУ¬
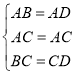 £¬
£¬
¡à![]()
![]() £¬
£¬
¡à![]() £»
£»
£š2£©²»±ä£¬![]() £¬ÀíÓÉÈçÏ£º
£¬ÀíÓÉÈçÏ£º
Á¬œÓ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() Óë
Óë![]() œ»ÓÚµã
œ»ÓÚµã![]() £¬
£¬
¡ß![]() £¬
£¬![]() £¬
£¬
¡à![]() ΪµÈ±ßÈýœÇÐΣ¬
ΪµÈ±ßÈýœÇÐΣ¬
¡ßËıßÐÎ![]() ÊÇÆœÐÐËıßÐΣ¬
ÊÇÆœÐÐËıßÐΣ¬
![]() £¬
£¬![]() £¬
£¬
¡ß![]() £¬
£¬
![]() £¬
£¬
¡ß![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
¡ß![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬
ͬÀí¿ÉµÃ£¬![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬
¡ß![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
¡ß![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
¡ß![]() £¬
£¬![]() £¬
£¬
£š3£©![]() £®
£®