题目内容
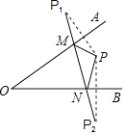
【题目】直线AB∥CD，点M，N分别在直线AB，CD上，点E为平面内一点．
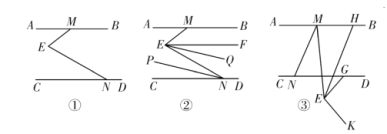
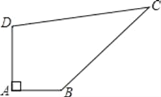
(1)如图①，探究∠AME，∠MEN，∠ENC的数量关系，并说明理由；
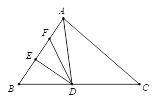
(2)如图②，∠AME=30°，EF平分∠MEN，NP平分∠ENC，EQ∥NP，求∠FEQ的度数；
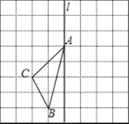
（3）如图③，点G为CD上一点，∠AMN=m∠EMN，∠GEK=m∠GEM，EH∥MN交AB于点H，直接写出∠GEK，∠BMN，∠GEH之间的数量关系(用含m的式子表示)．
【答案】（1）∠MEN=∠AME+∠ENC，见解析；（2）∠FEQ=15°；（3）∠BMN+∠GEK-m∠GEH=180°．
【解析】
（1）过点E作l∥AB，利用平行线的性质可得∠1=∠BME，∠2=∠DNE，由∠MEN=∠1+∠2，等量代换可得结论；
（2）利用角平分线的性质可得∠NEF=
∠MEN，∠ENP=∠END，由EQ∥NP，可得∠QEN=∠ENP=∠ENC，由（1）的结论可得∠MEN=∠AME+∠ENC，等量代换得出结论；
（3）由已知可得∠EMN=
∠BMN，∠GEN=∠GEK，由EH∥MN，可得∠HEM=∠ENM=
∠AMN，因为∠GEH=∠GEM-∠HEM，等量代换得出结论．
解：(1)过点E作l∥AB，
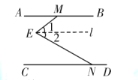
∵AB∥CD，∴l∥AB∥CD
∴∠1=∠AME，∠2=∠CNE．
∵∠MEN=∠1+∠2，
∴∠MEN=∠AME+∠ENC；
（2）∵EF平分∠MEN，NP平分∠ENC，
∴∠NEF=∠MEN，∠ENP=∠ENC．
∵EQ∥NP，∴∠QEN=∠ENP=∠ENC．
由（1）可得∠MEN=∠AME+∠ENC，∴∠MEN-∠ENC=∠AME=30°．
∴∠FEQ=∠NEF-∠NEQ=（∠MEN-∠ENC）=×30°=15°；
(3)∠BMN+∠GEK-m∠GEH=180°．理由如下：
∵∠AMN=m∠EMN，∠GEK=m∠GEM，
∴∠EMN=∠AMN，∠GEM=∠GEK．
∵EH∥MN，∴∠HEM=∠EMN=∠AMN．
∵∠GEH=∠GEM-∠HEM=∠GEK-∠AMN，
∴m∠GEH=∠GEK-∠AMN．
∵∠BMN+∠AMN=180°，
∴∠BMN+∠GEK-m∠GEH=180°．
