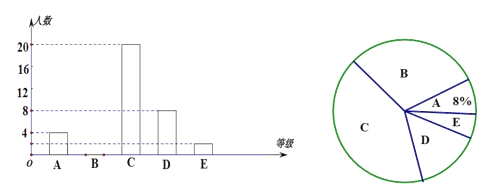
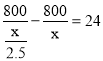题目内容
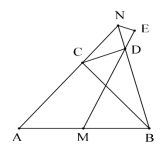
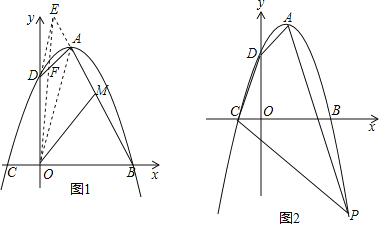
【题目】如图,△ABC内接于⊙O,点D为⊙O上一点,连接BD、AD、CD,AD交BC于点E,作AG⊥CD于点G交BC于点F,∠ADB=∠ABC.
(1)如图1,求证:AB=AC;
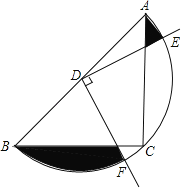
(2)如图2.若BC为直径,求证:EF2=BE2+CF2
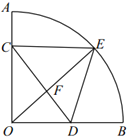
(3)如图在(1)的条件下,若∠ADC=60°,6CE=5BF,DG=![]() ,求⊙O的半径长.
,求⊙O的半径长.

【答案】(1)详见解析;(2)详见解析;(3)圆O的半径为![]() .
.
【解析】
(1)只需说明∠ABC=∠ACB即可;
(2)将△AFC绕点A顺时针旋转90°至△AHB,连接HE,再证明△AHE和△AFE全等,在Rt△BHE中由勾股定理即可得出结论;
(3)首先证明△ABC是等边三角形,再证明AD=BD+CD,接着通过计算得出BE、EF、FC三条线段之比,注意到∠BDC=120°,解三角形BDC可求出BC长度,利用垂径定理即可求得半径长度.
(1)证明:∵∠ADB=∠ACB,∠ADB=∠ABC,
∴∠ABC=∠ACB,
∴AB=AC;
(2)∵BC是直径,
∴∠BAC=90°,
∵AB=AC,
∴∠ABC=∠ACB=45°,
如图2,将△AFC绕点A顺时针旋转90°至△AHB,连接HE.
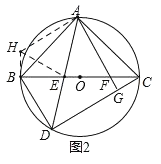
则BH=CF,∠ABH=∠ACF=45°,∠FAC=∠HAB,AH=AF,
∴∠HBE=∠ABH+∠ABC=90°,
∵AG⊥CD于G,
∴∠AGD=90°,
∵∠ADC=∠ABC=45°,
∴∠DAG=45°,
∴∠FAC+∠BAE=∠BAC-∠DAG=90°-45°=45°,
∴∠BAH+∠BAE=45°,即∠HAE=45°,
∴∠HAE=∠FAE,
在△AHE和△AFE中:
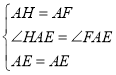 ,
,
∴△AHE≌△AFE(SAS),
∴HE=FE,
在Rt△BHE中,由勾股定理有:HE2=BH2+BE2,
∴EF2=CF2+BE2;
(3)∵∠ADB=∠ABC=∠ACB=∠ADC=60°,
∴△ABC是等边三角形,
如图3,延长DC至N,使CN=BD,连接AN,
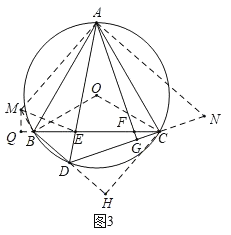
∵∠ABD+∠ACD=∠ACD+∠ACN=180°,
∴∠ABD=∠ACN,
在△ABD和△ACN中:
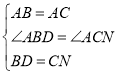 ,
,
∴△ABD≌△ACN(SAS),
∴AD=AN,
∵∠ADC=60°,
∴△ADN是等边三角形,
∴AD=DN=DC+CN=DC+BD.
将△AFC绕点A顺时针旋转60°至△AMB,连接EM,
则∠MBA=∠FCA=60°,∠MAB=∠FAC,AM=AF,MB=CF,
∵AG⊥DC于G,∠ADC=60°,
∴∠EAF=30°,
∴AD=2DG,
∴∠BAE+∠FAC=∠BAC﹣∠EAF=30°,
∴∠BAE+∠BAM=30°,即∠MAE=∠FAE=30°,
在△MAE和△FAE中:
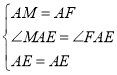 ,
,
∴△MAE≌△FAE(SAS),
∴ME=FE,
作MQ⊥BC于Q,
∵∠MBE=∠MBA+∠ABE=120°,
∴∠MBQ=60°,
设BE=x,CF=BM=y,
则BQ=![]() ,MQ=
,MQ=![]() ,
,
∴QE=BQ+BE=![]() +x,
+x,
∴ME=![]() =
=![]() ,
,
∴EF=ME=![]() ,
,
∵6CE=5BF,
∴6(y+![]() )=5(
)=5(![]() +x),
+x),
∴![]() =6y﹣5x,
=6y﹣5x,
整理得:(3x﹣5y)(8x﹣7y)=0,
∵x>y,所以3x=5y,
设x=5k,y=3k,则EF=![]() 7k,
7k,
∴AC=BC=BE+EF+CF=15k,
∵∠DBE=∠DAC,∠BDE=∠ADC=60°,
∴△DBE△DAC,
∴![]() ,
,
∴AD=3BD,
又∵BD+CD=AD,
∴CD=2BD,
∴CD=![]() AD,
AD,
∵DG=![]() AD=
AD=![]() ,
,
∴AD=![]() ,
,
∴BD=![]() AD=
AD=![]() ,CD=
,CD=![]() AD=
AD=![]() ,
,
作CH⊥BD于H,则∠CHD=90°,∠CDH=180°﹣∠CDB=60°,
∴DH=![]() CD=
CD=![]() ,CH=
,CH=![]() DH =
DH =![]() ,
,
所以BH=BD+DH=![]() ,
,
所以CB=![]() =8,
=8,
连接OB、OC,则OB=OC,∠BOC=2∠BAC=120°,
作OP⊥BC于P,∠BOP=![]() ∠BOC=60°,BP=
∠BOC=60°,BP=![]() BC=4,
BC=4,
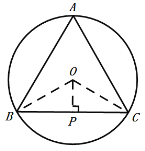
∴OB=![]() =
=![]() =
=![]() ,即圆O的半径为
,即圆O的半径为![]() .
.