��Ŀ����
����Ŀ����ͼ�������Ľ�����������AED�;���ABCD���ɣ����εij�BCΪ8m����ABΪ2m����BC���ڵ�ֱ��Ϊx�ᣬ�߶�BC���д���Ϊy�ᣬ����ƽ��ֱ������ϵ��y���������ߵĶԳ��ᣬ����E������ԭ��O�ľ���Ϊ6m�� 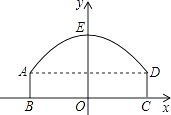
��1���������ߵĽ���ʽ��
��2��һ�����˿�����4.5m����2.4m������ͨ����������
��3���������������˫�е���Ϊ�˰�ȫ��������������м�����0.4m�ĸ��������������˿�������ͨ��������
���𰸡�
��1���⣺
������һ���������⣬A����4��2����D��4��2����E��0��6����
�������ߵĽ���ʽΪy=ax2+6��a��0������A����4��2����D��4��2�������
16a+6=2��
�� ![]() ��
��
�����ߵĽ���ʽΪy=�� ![]() x2+6��
x2+6��
���������������ʽΪy=ax2+bx+c��a��0����
����A��D��E��������� 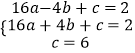
�� ![]() ��b=0��c=6��
��b=0��c=6��
�����ߵĽ���ʽΪy= ![]() x2+6
x2+6
��2���⣺�������⣬��x=��1.2�������ʽ��
��y=5.64��
��5.64��4.5������˿�����ͨ��
��3���⣺�������⣬x=��0.2��2.4=��2.6��x=0.2+2.4=2.6��
��x=��2.6�������ʽ��
��y=4.31��
��4.31��4.5��
����˿�������ͨ��
�������������ߵ����⣬һ�㶼Ҫ����ֱ������ϵ�����йس���ת��Ϊ������꣬�����ʽ�����ý���ʽ���ʵ�����⣮

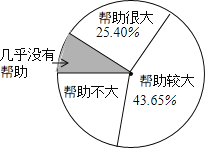
����Ŀ��Ϊ�˽⡰��ѧ˼�����Ķ�ѧϰ��ѧ�����ж��һ�о�Ա�����ȡ��һ�������ĸ�У��һѧ���������ʾ����飬��������õ������������������ͼ�ͱ�����ʾ��ͼ������û������ɣ���
ѡ�� | �����ܴ� | �����ϴ� | �������� | ����û�а��� |
���� | a | 543 | 269 | b |
����ͼ�����ṩ����Ϣ��
��1�����ʣ���ι��ж�����ѧ���������ʾ����飿
��2���������a��b��ֵ��
��ע���������漰���ġ�����������ȷ��1��