题目内容
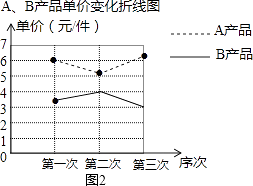
【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价(元/件) | 6 | 5.2 | 6.5 |
B产品单价(元/件) | 3.5 | 4 | 3 |
并求得了A产品三次单价的平均数和方差:![]() =5.9,SA2=
=5.9,SA2= ![]() [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]= ![]()
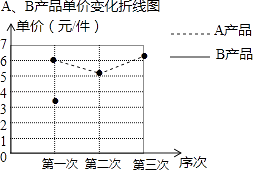
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
【答案】
(1)解:如图2所示:
(2)解: ![]() =
= ![]() (3.5+4+3)=3.5,S
(3.5+4+3)=3.5,S ![]() =
= ![]() =
= ![]() ,
,
∵B产品的方差小,
∴B产品的单价波动小;
(3)解:第四次调价后,对于A产品,这四次单价的中位数为 ![]() =
= ![]() ;
;
对于B产品,∵m>0,
∴第四次单价大于3,
∵第四次单价小于4,
∴ ![]() ×2﹣1=
×2﹣1= ![]() ,
,
∴m=25.
【解析】(1)依据表示中B产品的单价补全折线统计图即可;
(2)分别依据平均数公式和方差公式进行计算即可;
(3)首先确定这四次单价的中位数,然后确定第四次调价的范围,最后再根据“A产品这四次单价的中位数是B产品四次单价中位数的2倍少1”列出关于m的方程,从而可求得m的值.

【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表).
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
t≤150 | 150<t<350 | t=350 | t>350 | |
方式一计费/元 | 58 | 108 | ||
方式二计费/元 | 88 | 88 | 88 |
(2)当t为何值时,两种计费方式的费用相等?
(3)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可).