题目内容
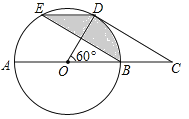
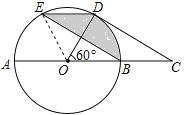
【题目】如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O的切线CD交AB的延长线于点C，E为
的中点，连接DE，EB．
（1）求证：四边形BCDE是平行四边形；
（2）已知图中阴影部分面积为6π，求⊙O的半径r．
【答案】（1）证明见试题解析；（2）6．
【解析】
试题分析：（1）先证明DE∥BC，再由CD是⊙O的切线，得到OD⊥CD，于是得到BE∥CD，即可证得结论；
（2）连接OE，由（1）知，
，得到∠BOE=120°，根据扇形的面积公式列方程即可得到结论．
试题解析：（1）∵∠BOD=60°，∴∠AOD=120°，∴
，∵E为
的中点，∴，∴DE∥AB，OD⊥BE，即DE∥BC，∵CD是⊙O的切线，∴OD⊥CD，∴BE∥CD，∴四边形BCDE是平行四边形；
（2）连接OE，由（1）知，，∴∠BOE=120°，∵阴影部分面积为6π，∴
，∴r=6．
练习册系列答案
相关题目
【题目】某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了单价变化不完整的统计表及折线图．
A，B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价（元/件） | 6 | 5.2 | 6.5 |
B产品单价（元/件） | 3.5 | 4 | 3 |
并求得了A产品三次单价的平均数和方差：
=5.9，SA2= 
[（6﹣5.9）2+（5.2﹣5.9）2+（6.5﹣5.9）2]= 
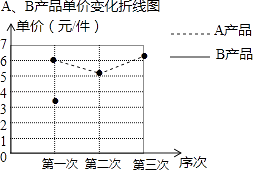
（1）在折线图中画出B产品的单价变化的情况；
（2）求B产品三次单价的方差；
（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件的基础上调m%（m＞0），但调价后不能超过4元/件，并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．