题目内容
已知线段AB=4,点C是平面上一点(不与A,B重合),M、N分别是线段CA,CB的中点.
(1)当C在线段AB上时,如图,求MN的长;
(1)当C在线段AB的延长线上时,画出图形,并求MN长;
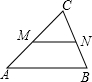
(2)当C在直段AB外时,画出图形,量一量,写出MN的长(不写理由)
(1)当C在线段AB上时,如图,求MN的长;

(1)当C在线段AB的延长线上时,画出图形,并求MN长;
(2)当C在直段AB外时,画出图形,量一量,写出MN的长(不写理由)
分析:(1)求出CM=
AC,CN=
BC,即可得出MN=
AB,求出即可;
(2)画出图形,求出MN=
(AC-BC)=
AB,求出即可;
(3)画出图形,量出MN长即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)画出图形,求出MN=
| 1 |
| 2 |
| 1 |
| 2 |
(3)画出图形,量出MN长即可.
解答:解:(1)∵M、N分别是CA、CB的中点,
∴CM=
AC,CN=
BC,
又∵AB=4,
∴MN=
(AC+BC)=
AB=2.
(2)如图:
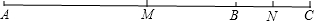
∵M、N分别是CA、CB的中点,
∴CM=
AC,BN=
BC,
又∵AB=4,
∴MN=CM-CN=
(AC-BC)=
AB=2.
(3)
测量可得MN=2.
∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=4,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图:
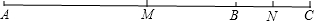
∵M、N分别是CA、CB的中点,
∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=4,
∴MN=CM-CN=
| 1 |
| 2 |
| 1 |
| 2 |
(3)

测量可得MN=2.
点评:本题考查了两点间的距离的应用,主要考查学生的理解能力、画图能力和计算能力.

练习册系列答案
相关题目