题目内容
【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
【答案】(1)30秒;(2)0.6秒;(3)![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)设两车经过x秒相遇,根据相遇时,两车行驶的路程之和等于隧道的长列出方程,解方程即可;
(2)设两车从相遇到完全离开所需的时间为y秒,等量关系为:速度和×时间=两车的车长之和,依此列出方程,解方程即可;
(3)先根据小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍,求出两车相遇后一共行驶的路程之和,再除以速度和即可.分两种情况进行讨论:①车尾相遇前;②车尾相遇后.
(1)设两车经过x秒相遇,根据题意得:
(10+30)x=1200
解得:x=30.
答:两车经过30秒相遇;
(2)设两车从相遇到完全离开所需的时间为y秒,根据题意得:
(10+30)y=4+20
解得:y=0.6.
答:两车从相遇到完全离开所需的时间为0.6秒;
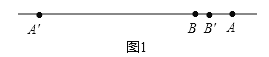
(3)设AB表示车长为4米的小轿车,其中点A表示车头,点B表示车尾,A'B'表示车长为20米的大货车,其中点A'表示车头,点B'表示车尾,则AB=4米,A'B'=20米,设BB'=a米.
分两种情况:①车尾相遇前,如图1,则AB'=(4﹣a)米.
小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时,AA'=4BB',所以20+4﹣a=4a,解得:a![]() ,则AA'
,则AA'![]() ,故所求时间为:
,故所求时间为:![]() (10+30)
(10+30)![]() (秒);
(秒);
②车尾相遇后,如图2,则AB'=(4+a)米.
小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时,AA'=4BB',所以20+4+a=4a,解得:a=8,则AA'=32,故所求时间为:32÷(10+30)![]() (秒).
(秒).

综上所述:当小轿车车头和大货车车头相遇后,小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间为![]() 秒或
秒或![]() 秒.
秒.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案