��Ŀ����
��ͼ��A��B��C��D���ĸ�С��������֮���B��C�ⶼ�б�ֱ�Ĺ�·�����ӣ����й�·BD��AC��ֱ������������ʻ�ڳ���֮�䣬��Ʊ����·�̳����ȣ���֪������Ĺ�������Ʊ�����£�A?B��7.5Ԫ��A?C��12.5Ԫ��B?D��6Ԫ��Ϊ�˷���B��C��������������ƻ���B��C֮�佨��һ����ֱ�Ĺ�·�����ʣ�����·�ɺ�������B��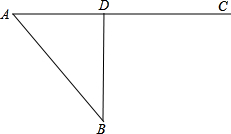 C�����Ĺ���������Ʊ��Ӧ��Ϊ���ٲź��ʣ�˵˵������ɣ�
C�����Ĺ���������Ʊ��Ӧ��Ϊ���ٲź��ʣ�˵˵������ɣ�
�������������⣬�������BC���ȵ�һ�κ�����ϵʽ���ú�k�Ĵ���ʽ��ʾ�����߶Σ���ɣ�
���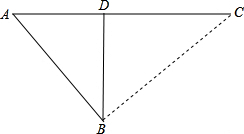 �⣺����BC����Ʊ��ΪyԪ��·��Ϊx����y=kx��
�⣺����BC����Ʊ��ΪyԪ��·��Ϊx����y=kx��
���������AB=
��AC=
��BD=
����1�֣�
��BD��AC��
��AD2=AB2-BD2��
AD=
��
��AD=
����2�֣�
��DC=AC-AD=
����3�֣�
����Rt��BDC��
BC2=BD2+DC2��
��BC=
��BC=
����5�֣�
��B��C�����Ĺ���������Ʊ��Ӧ��Ϊ10Ԫ����6�֣�
 �⣺����BC����Ʊ��ΪyԪ��·��Ϊx����y=kx��
�⣺����BC����Ʊ��ΪyԪ��·��Ϊx����y=kx�����������AB=
| 7.5 |
| k |
| 12.5 |
| k |
| 6 |
| k |
��BD��AC��
��AD2=AB2-BD2��
AD=
(
|
��AD=
| 4.5 |
| k |
��DC=AC-AD=
| 8 |
| k |
����Rt��BDC��
BC2=BD2+DC2��
��BC=
(
|
��BC=
| 10 |
| k |
��B��C�����Ĺ���������Ʊ��Ӧ��Ϊ10Ԫ����6�֣�
����������Ӧ�õķ�����Ϊ����������߶εij����ú�k�Ĵ���ʽ��ʾ���������������k��ֵ����һ�����⣮

��ϰ��ϵ�д�
�����Ŀ
 14����ͼ����֪��P�İ뾶OD=5��OD��AB��������G��OG=3������AB=
14����ͼ����֪��P�İ뾶OD=5��OD��AB��������G��OG=3������AB= ��ͼ����֪A��B�����Ƿ���������y=
��ͼ����֪A��B�����Ƿ���������y=

 ��ͼAB�ǡ�O��ֱ������O��BC���е�D����DE��AC�ڵ�E��
��ͼAB�ǡ�O��ֱ������O��BC���е�D����DE��AC�ڵ�E��