题目内容
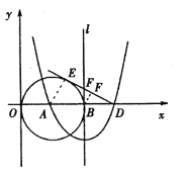
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
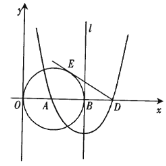
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
【答案】(1)y=![]() (x-6)2-3;(2)DE=3
(x-6)2-3;(2)DE=3![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)由题意可知,抛物线的对称轴为直线x=6,可设抛物线的解析式为y=a (x-6)2+k,将A,C两点坐标代入求a,k,即可确定该抛物线的解析式;(2)连接AE,可知∠AED=90°,AE=3 ,因为直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,所以AB=BD=3, AD=6 ,于是利用勾股定理可求出DE的长;(3)由题意可知,利用有两个角对应相等的两个三角形相似,切线DE上符合条件的F点有两个,即当BF⊥ED时和FB⊥AD时,利用相似三角形性质即可求出BF的长.
试题解析:(1)由题意可知,抛物线的对称轴为直线x=6,∴设抛物线的解析式为y=a (x-6)2+k,∵抛物线经过点A(3,0)和C(0,9),∴将A,C两点坐标代入得:![]() ,解得:a=
,解得:a=![]() ,k=-3.∴抛物线的解析式为y=
,k=-3.∴抛物线的解析式为y=![]() (x-6)2-3;(2)连接AE,∵DE是⊙A的切线,∴∠AED=90°,AE=3 ,∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,∴AB=BD=3,∴AD=6 , 在Rt△ADE中,DE2=AD2-AE2=62-32=27,∴DE=3
(x-6)2-3;(2)连接AE,∵DE是⊙A的切线,∴∠AED=90°,AE=3 ,∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,∴AB=BD=3,∴AD=6 , 在Rt△ADE中,DE2=AD2-AE2=62-32=27,∴DE=3![]() ;
;
(3)利用有两个角对应相等的两个三角形相似,当BF⊥ED时,∵∠AED=∠BFD=90°,∠ADE=∠BDF,∴△AED∽△BFD,∴![]() ,即
,即![]() ,∴BF=
,∴BF=![]() .当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD , ∴
.当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD , ∴![]() 即BF=
即BF=![]()
![]() ,∴当△BFD与△EAD相似时,BF的长为
,∴当△BFD与△EAD相似时,BF的长为![]() 或
或![]() .
.