��Ŀ����
����Ŀ����ͼ1��һ����Ϊ ![]() ����Ϊ
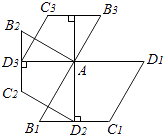
����Ϊ ![]() �ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ���������������Σ���ͼ2����
�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ���������������Σ���ͼ2����

��1��ͼ2�е���Ӱ���ֵ����Ϊ ��
��2���۲�ͼ2����д�� ![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵ�� ��
֮��ĵ�����ϵ�� ��
��3�����ݣ�2���еĽ��ۣ��� ![]() ��
��![]() ����
���� ![]() ��
��
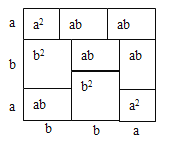
��4��ʵ�������ǿ�����ͼ�ε������ʾ������ʽ�������������һ������ͼ������ʾ���ʽ![]() ����ͼ���ϰ�ÿһ���ֵ������д�����
����ͼ���ϰ�ÿһ���ֵ������д�����
���𰸡���1��![]() ����2��
����2��![]() ����3����5����4���������
����3����5����4���������
��������
��1����ʾ����Ӱ���������εı߳���Ȼ����������ε������ʽ��ʽ���ɣ�
��2�����ݴ������ε������ȥС�����ε���������ĸ�С�����ε������ʽ���ɣ�
��3������x-y��2����Ϊ��x+y��2��4xy���ٴ�����ֵ���ɣ�
��4������֪�ĺ��ʽ��������Ӧ��ͼ�Σ���ͼ��ʾ��
�⣺��1����Ӱ����Ϊһ�������Σ���߳�Ϊb-a��
���������![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���������������![]()
С���������Ϊ��![]() =
=![]() ��
��
�����ĸ������ε����Ϊ��![]() ��
��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3���ɣ�2��֪��![]() ��
��
��![]() ��
��
��![]() =
=![]() ��
��
�ʴ�Ϊ����5��
��4�����ϵ�ʽ![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��

 ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�