题目内容
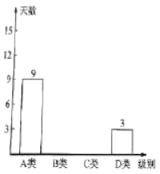
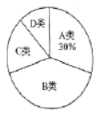
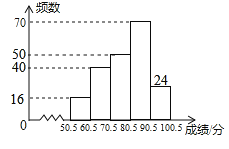
【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩（得分数取正整数，满分为
分）进行统计，绘制统计图如下（未全完成），已知
组的频数比
组小
，解答下列问题：
（1）求样本容量及频数分布直方图中的
，
的值；
（2）扇形统计图中，
部分所对的圆心角为
，求
的值并补全频数分布直方图；
（3）若成绩在
分以上优秀，全校共有
名学生估计成绩优秀的学生有多少名？
【答案】（1）
，
；（2）126°，补图见解析；（3）940名
【解析】
（1）由于A组的频数比B组小24，而A组的频率比B组小12%，则可计算出调查的总人数，然后计算a和b的值；
（2）用360度乘以D组的频率可得到n的值，然后计算出C和E组的频数后补全频数分布直方图；
（3）利用样本根总体，用2000乘以D组和E组的频率和即可．
解：（1）样本容量：
，
，
．
（2）
类
，
（3）
（名）
即全校成绩优秀的学生有
名．
练习册系列答案
相关题目
【题目】某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，种植花卉的利润y2与投资量x的平方成正比例关系，并得到了表格中的数据．
投资量x（万元） | 2 |
种植树木利润y1（万元） | 4 |
种植花卉利润y2（万元） | 2 |
（1）分别求出利润y1与y2关于投资量x的函数关系式；
（2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．
