Question

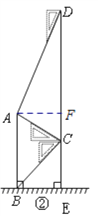
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑（如图①）.为了测量雕塑的高度，小明在二楼找到一点C，利用三角板测得雕塑顶端A点的仰角为，底部B点的俯角为，小华在五楼找到一点D，利用三角板测得A点的俯角为（如图②）.若已知CD为10米，请求出雕塑AB的高度．（结果精确到0.1米，参考数据）．

Answer 1

【答案】

【解析】试题分析：

由题意可得:∠ADC=30°，∠ACD=60°，∠BCE=45°，∠ABE=∠BEC=90°，由此可得∠DAC=180°-30°-60°=90°，结合CD=10可得AC=5；过点A作AF⊥DE于点F，则∠AFE=90°，从而在△AFC中由∠ACD=60°可得∠CAF=30°，由此可得CF=2.5，AF=，再证四边形ABEF是矩形可得BE=AF=，结合∠BCE=45°，∠BEC=90°可得CE=BE=，从而可得AB=EF=CF+BE=2.5+.

试题解析：

由题意可得:∠ADC=30°，∠ACD=60°，∠BCE=45°，∠ABE=∠BEC=90°，

∴在△ADC中，∠DAC=180°-30°-60°=90°，

又∵CD=10，∠D=30°，

∴AC=5，

过点AF⊥CD于点F，

∴∠AFC=90°，

∵∠ACD=60°，

∴∠CAF=30°，

∴CF=2.5，AF=AC·sin60°=，

∵∠ABE=∠BEF=∠AFE=90°，

∴四边形ABEF是矩形，

∴BE=AF=，AB=EF，

∵在△BEC中，∠BEC=90°，∠BCE=45°，

∴CE=BE=，

∴AB=EF=CE+CF=2.5+ 6.8.