题目内容
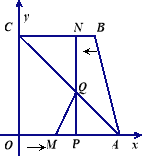
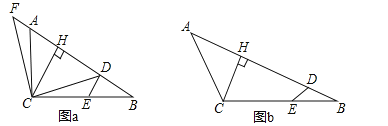
【题目】把一副三角板如图甲放置,其中![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,
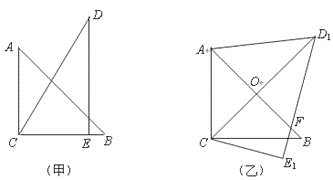
,![]() .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点![]() ,与D1E1相交于点F.
,与D1E1相交于点F.
(1)求![]() 的度数;
的度数;
(2)求线段AD1的长;
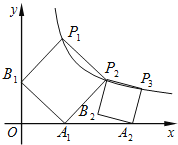
(3)若把三角形D1CE1绕着点![]() 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
【答案】(1)1200 (2)5 (3)内部
【解析】
试题(1)根据OFE1=∠B+∠1,易得∠OFE1的度数;(2)在Rt△AD1O中根据勾股定理就可以求得AD1的长;(3)设BC(或延长线)交D2E2于点P,Rt△PCE2是等腰直角三角形,就可以求出CB的长,判断B在△D2CE2内.
试题解析:
(1)如图所示,![]() ,
,![]() ,
,
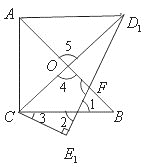
∴![]() .
.
又![]() ,
,
∴![]() .
.
(2)![]() ,∴∠D1FO=60°.
,∴∠D1FO=60°.
![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() .
.
![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() .
.
(3)点![]() 在
在![]() 内部.
内部.
理由如下:设![]() (或延长线)交
(或延长线)交![]() 于点P,则
于点P,则![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,即
,即![]() ,∴点
,∴点![]() 在
在![]() 内部.
内部.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目