Question

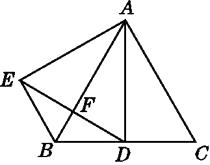
【题目】如图，已知□ABCD中，DE是∠ADC的角平分线，交BC于点E ．

（1）求证：CD=CE；
（2）若BE=CE ， 求证：AE⊥DE.

Answer 1

【答案】
（1）证明：∵ 四边形ABCD是平行四边形，
∴ AD∥BC ，
∴ ∠ADE=∠DEC.
∵ DE是∠ADC的角平分线，
∴ ∠ADE=∠CDE ，
∴ ∠CDE=∠DEC ，
∴ CD=CE
（2）证明：∵ 四边形ABCD是平行四边形，
∴ AB=DC.
∵ CD=CE ， BE=CE
∴ AB=BE,
∴ ∠BAE=∠BEA.
∵ AD∥BC ，
∴ ∠DAE=∠BEA.
∴ ∠DAE=∠BAE= ∠BAD.
∵ AB∥DC ，
∴ ∠BAD+∠ADC=180°，
∵ ∠ADE= ∠ADC ，
∴ ∠DAE+∠ADE= (∠BAD+∠ADC)=90°，
∴ ∠AED=90°,
∴ AE⊥DE.
【解析】（1）先依据角平分线的定义和平行线的性质可证明∠CDE=∠DEC，最后，依据等角对等边的性质进行证明即可；
（2）先证明BE=AB，可得到∠BAE=∠BEA，然后可证明∠BAE=∠DAE，从而可证明∠EAD+∠ADE=(∠BAD+∠ADC)=90°，然后可证明∠AED=90°.