题目内容
【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )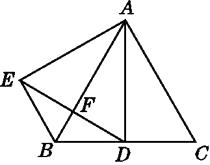
A.3
B.2
C.1
D.0
【答案】A
【解析】∵△ABC是等边三角形,
∴AB=AC,
又∵AD是∠BAC的平分线,
∴AD⊥BC,BD=DC,
∵△ABC和△ADE是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,
∴∠BAE=∠DAC,
在△BAE和△CAD中,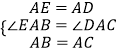
∴△BAE≌△CAD(SAS),
∴∠DAC=∠BAE,BE=DC,
又∵BD=DC,
∴BE=BD,
∵△ABC是等边三角形,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠DAC=30°,
∴∠BAE=30°,
∵△ADE是等边三角形,
∴∠DAE=60°,
∴∠BAD=30°=∠BAE,
∵AE=AD,
∴EF=DF(三线合一),
即①②③都符合题意。
故应选:A 。
【考点精析】关于本题考查的等腰三角形的性质和等边三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角);等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
【题目】NBA季后赛正如火如荼地进行着,詹姆斯率领的骑士队在第三场季后赛中先落后25分的情况
下实现了大逆转.该场比赛中詹姆斯的技术统计数据如下表所示:
技术 | 上场时间 (分钟) | 出手投篮(次) | 投中 (次) | 罚球 得分 | 篮板 (个) | 助攻 (次) | 个人 总得分 |
数据 | 45 | 27 | 14 | 7 | 13 | 12 | 41 |
【注:表中出手投篮次数和投中次数均不包括罚球,个人总得分来自2分球和3分球的得分以及罚
球得分.】根据以上信息,求出本场比赛中詹姆斯投中2分球和3分球的个数.