题目内容
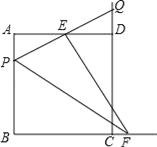
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为![]() 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;

(3)连接OE交BC于点F,若AB=![]() ,求OE的长度.
,求OE的长度.
【答案】(1)45°; (2)见解析 (3)![]()
【解析】(1)连接AD,由D为弧AB的中点,得到AD=BD ,根据圆周角定理即可得到结论;
(2)由已知条件得到∠CBE=45°,根据圆内接四边形的性质得到∠A=∠BD,根据相似三角形的性质得到DE:AC=BE:BC,即可得出结论.
(3)连接CO,根据线段垂直平分线的判定定理得到OE垂直平分BC,由三角形的中位线到现在得到OF=![]() AC,根据直角三角形的性质得到EF=
AC,根据直角三角形的性质得到EF=![]() BC,由勾股定理即可得到结论.
BC,由勾股定理即可得到结论.
(1)解:连接AD,
∵D为弧AB的中点,∴AD=BD,
∵AB为直径,∴∠ADB=90°,∴∠DAB=∠DBA=45°
∴∠DCB=∠DAB=45°;
(2)证明:∵BE⊥CD,又∵∠ECB=45°,∴∠CBE=45°,∴CE=BE,
∵四边形ACDB是圆O的内接四边形,∴∠A+∠BDC=180°,
又∵∠BDE+∠BDC=180°,∴∠A=∠BDE,
又∵∠ACB=∠BED=90°,∴△ABC∽△DBE,
∴DE:AC=BE:BC,∴DE:BE=AC:BC=1:2,
又∵CE=BE,∴DE:CE=1:2,∴D为CE的中点;
(3)解:连接CO,∵CO=BO,CE=BE,∴OE垂直平分BC,
设OE交BC于F,则F为BC中点,又∵O为AB中点,∴OF为△ABC的中位线,
∴OF=![]() AC,
AC,
∵∠BEC=90°,EF为中线,∴EF=![]() BC,
BC,
在Rt△ACB中,AC2+BC2=AB2,
∵AC:BC=1:2,AB=![]() ,∴AC=
,∴AC=![]() ,BC=2
,BC=2![]()
∴OE=OF+EF=![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案