题目内容
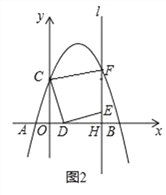
【题目】如图1，在平面直角坐标系中，抛物线y=ax2+bx+3交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，交抛物线于点M，过点C作CF⊥l于F．
（1）求抛物线解析式；
（2）如图2，当点F恰好在抛物线上时（与点M重合）
①求点F的坐标；
②求线段OD的长；
③试探究在直线l上，是否存在点G，使∠EDG=45°？若存在，请直接写出点G的坐标；若不存在，请说明理由．
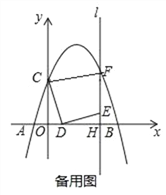
（3）在点D的运动过程中，连接CM，若△COD∽△CFM，请直接写出线段OD的长．
【答案】（1）y=
；（2）①（4，3）；②1；
③存在，点G的坐标为（4，6）或（4，﹣
）．理由见解析；（3）
或
．
【解析】分析：（1）先求得点C的坐标，设抛物线的解析式为y=a（x+1）（x﹣5），将点C的坐标代入求得a的值即可；（2）①由题意可知CF∥x轴，则点F纵坐标为3，将y=3代入抛物线的解析式可求得点F的横坐标；②先证明Rt△OCD≌Rt△HDE，从而得到CO=DH=3，然后由OH=4，可得到OD=1；③将CD绕点C逆时针旋转90°得到线段CN，则N（3，4）且四边形CDEN为正方形，然后可求得点N的坐标，接下来求得DG的解析式，然后可求得点G的坐标，由DG⊥DG′以及点D的坐标可求得DG′的解析式，然后可求得点G′的坐标；（3）设点D的坐标为（a，0），则点M的坐标（a+3，﹣
a2﹣
a+
），然后可求得FM的长，然后由△COD∽△CFM，可得到
，最后依据上述比例关系列出关于a的方程求解即可．
本题解析;
（1）把x=0代入抛物线的解析式得：y=3，∴C（0，3）．
设抛物线的解析式为y=a（x+1）（x﹣5），将点C的坐标代入得：﹣5a=3，解得：a=﹣
．
∴抛物线的解析式为y=
．
（2）①∵CF⊥l，OB⊥l，
∴CF∥x轴．
∴点F的纵坐标为3．
将y=3代入抛物线的解析式得：﹣
x2+
x+3=3，解得x=0或x=4．
∴点F的坐标为（4，3）．
②∵点F的坐标为（4，3），
∴点H的坐标为（4，0）．
∵∠CDE=90°，
∴∠CDO+∠EDH=90°．
∵∠OCD+∠CDO=90°，
∴∠OCD=∠EDH．
由旋转的性质可知：CD=DE．
在Rt△OCD和Rt△HDE中，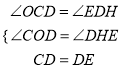 
，
∴Rt△OCD≌Rt△HDE．
∴CO=DH=3．
又∵OH=4，
∴OD=1．
③如图1所示：将CD绕点C逆时针旋转90°得到线段CN，则N（3，4）且四边形CDEN为正方形．
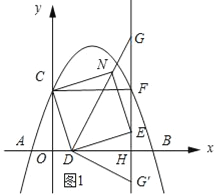
∵四边形CDEN为正方形，
∴∠GDE=45°．
设DN的解析式为y=kx+b，将点D和点N的坐标代入得： 
，解得：k=2，b=﹣2．
∴DN的解析式为y=2x﹣2．
把x=4代入得：y=6，
∴G（4，6）．
设直线DG′的解析式为y=﹣
x+c，将点D的坐标代入得：﹣
+c=0，解得：c=
．
∴直线DG′的解析式为y=﹣
x+
．
将x=4代入得：y=﹣
．
∴点G′的坐标为（4，﹣
）．
综上所述，点G的坐标为（4，6）或（4，﹣
）．
（3）如图2所示：
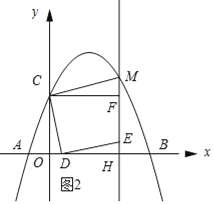
设点D的坐标为（a，0），则点M的坐标（a+3，﹣
a2﹣
a+
）．
∴FM=﹣
a2﹣
a+
．
∵△COD∽△CFM，
∴
，即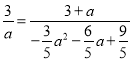
，
整理得：14a2+33a﹣27=0，解得a=
或a=﹣3（舍去）．
∴OD=
．
如图3所示：
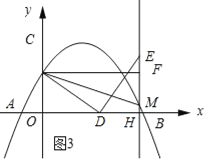
设点D的坐标为（a，0），则点M的坐标（a+3，﹣
a2﹣
a+
）．
∴FM=
a2+
a﹣
．
∵△COD∽△CFM，
∴
， 
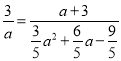，整理得：4a2+3a﹣27=9，解得：a=﹣3（舍去）或a=
．
∴OD=
．
综上所述，OD的长为
或
.
