题目内容
完成推理过程并填写推理理由:
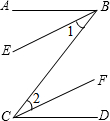
(1)已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.
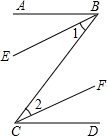
(2)如图,已知:∠BCF=∠B+∠F.求证:CD∥AB.

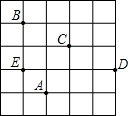
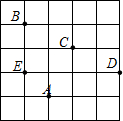
(3)如果点A的位置为(-1,0),那么点B,C,D,E的位置分别为______.
(1)证明:∵BE、CF分别平分∠ABC和∠BCD,
∴∠1=∠ABC∠2=∠BCD,
∵BE∥CF,
∴∠1=∠2,
∴∠ABC=∠BCD,即∠ABC=∠BCD,
∴AB∥CD;
(2)证明:经过点C画CD∥AB,
∴∠BCD=∠B,
∵∠BCF=∠B+∠F,∠BCF=∠BCD+∠DCF,
∴∠DCF=∠F,
∴CD∥EF,
∴AB∥EF;
(3)解:∵点A的位置为(-1,0),
∴可得出原点的位置如所示,
∴B点坐标为:(-2,3),
C点坐标为:(0,2),
D点坐标为:(2,1),
E点坐标为:(-2,1),
故答案为:(-2,3),(0,2),(2,1),(-2,1).
分析:(1)根据BE∥CF,得∠1=∠2,根据BE、CF分别平分∠ABC和∠BCD,得∠ABC=2∠1,∠BCD=2∠2,则∠ABC=∠BCD,根据内错角相等从而证明AB∥CD,
(2)根据两直线平行,得出∠BCD=∠B,再根据等式的性质得出∠DCF=∠F,再根据内错角相等即可判出CD∥EF,再根据平行于同一直线的两直线平行即可证出AB∥EF,
(3)运用点A的位置为(-1,0),可以确定原点的位置,结合原点的位置,可以得出B,C,D,E点的坐标.
点评:(1)本题考查了平行线的性质和判定以及角平分线的定义,
(2)本题考查了平行线的性质及平行线的判定,涉及到等式的性质等知识点,要求学生熟练掌握各定理及推论,
(3)本题主要考查了坐标确定位置,解决问题的关键是,找到原点,再确定各点的坐标.
∴∠1=∠ABC∠2=∠BCD,
∵BE∥CF,
∴∠1=∠2,
∴∠ABC=∠BCD,即∠ABC=∠BCD,
∴AB∥CD;
(2)证明:经过点C画CD∥AB,
∴∠BCD=∠B,
∵∠BCF=∠B+∠F,∠BCF=∠BCD+∠DCF,
∴∠DCF=∠F,
∴CD∥EF,
∴AB∥EF;
(3)解:∵点A的位置为(-1,0),
∴可得出原点的位置如所示,
∴B点坐标为:(-2,3),
C点坐标为:(0,2),
D点坐标为:(2,1),
E点坐标为:(-2,1),
故答案为:(-2,3),(0,2),(2,1),(-2,1).
分析:(1)根据BE∥CF,得∠1=∠2,根据BE、CF分别平分∠ABC和∠BCD,得∠ABC=2∠1,∠BCD=2∠2,则∠ABC=∠BCD,根据内错角相等从而证明AB∥CD,
(2)根据两直线平行,得出∠BCD=∠B,再根据等式的性质得出∠DCF=∠F,再根据内错角相等即可判出CD∥EF,再根据平行于同一直线的两直线平行即可证出AB∥EF,
(3)运用点A的位置为(-1,0),可以确定原点的位置,结合原点的位置,可以得出B,C,D,E点的坐标.
点评:(1)本题考查了平行线的性质和判定以及角平分线的定义,
(2)本题考查了平行线的性质及平行线的判定,涉及到等式的性质等知识点,要求学生熟练掌握各定理及推论,
(3)本题主要考查了坐标确定位置,解决问题的关键是,找到原点,再确定各点的坐标.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
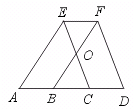 18、完成下列推理,并填写理由.
18、完成下列推理,并填写理由.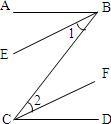

 完成推理过程并填写推理理由:
完成推理过程并填写推理理由: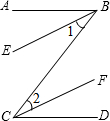 完成推理过程并填写推理理由:
完成推理过程并填写推理理由: ∠________∠2=
∠________∠2=