题目内容
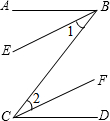 完成推理过程并填写推理理由:
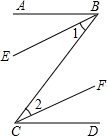
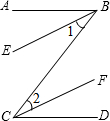
完成推理过程并填写推理理由:已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD
求证:AB∥CD.
证明:∵BE、CF分别平分∠ABC和∠BCD(已知)
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵BE∥CF(已知)∴∠1=∠2(两直线平行,内错角相等)
∴
| 1 |
| 2 |
| 1 |
| 2 |
即∠ABC=∠BCD,∴AB∥CD(内错角相等,两直线平行)
分析:根据角平分线的性质可求得∠1=
∠ABC,∠2=
∠BCD,又因为BE∥CF,所以有∠1=∠2,等量代换可知∠ABC=∠BCD,根据内错角相等,两直线平行即可证明.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵BE、CF分别平分∠ABC和∠BCD(已知),
∴∠1=
∠ABC∠2=
∠BCD(角平分线的定义),
∵BE∥CF(已知),
∴∠1=∠2(两直线平行,内错角相等),
∴
∠ABC=
∠BCD(等量代换),
∴∠ABC=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵BE∥CF(已知),
∴∠1=∠2(两直线平行,内错角相等),
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
点评:本题利用角平分线的性质、平行线的判定和性质求解,主要在于练习几何证明题的书写格式.解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
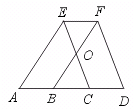 18、完成下列推理,并填写理由.
18、完成下列推理,并填写理由.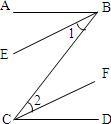


 完成推理过程并填写推理理由:
完成推理过程并填写推理理由: ∠________∠2=
∠________∠2=