题目内容
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.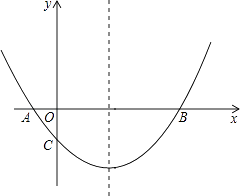
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0,- ![]() )三点在抛物线上,
)三点在抛物线上,
∴  ,
,
解得 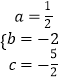 .
.
∴抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ;
;
(2)
解:∵抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ,
,
∴其对称轴为直线x=﹣ ![]() =﹣
=﹣ ![]() =2,
=2,
连接BC,如图1所示,
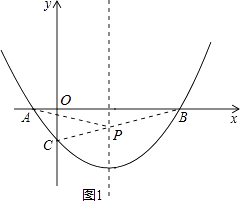
∵B(5,0),C(0,﹣ ![]() ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴ 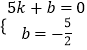 ,
,
解得 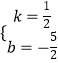 ,
,
∴直线BC的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当x=2时,y=1﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P(2,﹣ ![]() );
);
(3)
解:存在.
如图2所示,
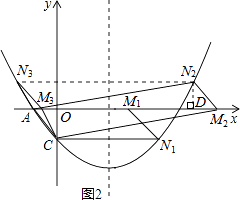
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,﹣ ![]() ),
),
∴N1(4,﹣ ![]() );
);
②当点N在x轴上方时,
如图,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
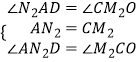
∴△AN2D≌△M2CO(ASA),
∴N2D=OC= ![]() ,即N2点的纵坐标为
,即N2点的纵坐标为 ![]() .
.
∴ ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() =
= ![]() ,
,
解得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴N2(2+ ![]() ,
, ![]() ),N3(2﹣
),N3(2﹣ ![]() ,
, ![]() ).
).
综上所述,符合条件的点N的坐标为(4,﹣ ![]() ),(2+
),(2+ ![]() ,
, ![]() )或(2﹣
)或(2﹣ ![]() ,
, ![]() ).
).
【解析】本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,- ![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
【考点精析】本题主要考查了确定一次函数的表达式和平行四边形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

【题目】油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下:
油电混动汽车 | 普通汽车 | |
购买价格 | 17.48 | 15.98 |
每百公里燃油成本(元) | 31 | 46 |
某人计划购入一辆上述品牌的汽车.他估算了未来10年的用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计平均每年行驶的公里数至少为( )
A. 5000 B. 10000 C. 15000 D. 20000