题目内容
【题目】如图,矩形ABCD的对角线AC与BD相交于点O,延长CB到点E,使BE=BC,连接AE.
(1)求证:四边形ADBE是平行四边形;
(2)若AB=4,OB=![]() ,求四边形ADBE的周长.
,求四边形ADBE的周长.
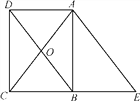
【答案】(1)见解析;(2)16.
【解析】试题分析:(1)依据矩形的性质可知AD∥BE,AD=BC,结合条件BE=CB可得到AD=BE,然后依据一组对边平行且相等的四边形是平行四边形进行证明即可;
(2)依据矩形的性质可得到AC=BD=2OB=4,由ADBE为平行四边形可知AE=5,在Rt△ABE中,依据勾股定理可求得BE的长,最后依据平行四边形ADBE的周长=2×(BE+AE)求解即可.
试题解析::(1)∵ABCD为矩形,
∴AD=BC,AD∥BC.
又∵BC=BE,
∴BE=AD.
∵AD∥BE,
∴四边形ADBE为平行四边形.
(2)∵ABCD为矩形,OB=![]() ,
,
∴AC=BD=5,∠ABE=90°
∵四边形ADBE为平行四边形,
∴AE=BD=5.
在Rt△ABE中,依据勾股定理可知:BE=![]() =3.
=3.
∴平行四边形ADBE的周长=2×(BE+AE)=2×(5+3)=16.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目