题目内容
阅读材料:已知方程p2-p-1=0,1-q-q2=0且pq≠1,求
的值.
解:由p2-p-1=0,及1-q-q2=0可知p≠0,q≠0又∵pq≠1,∴p≠
.
∵1-q-q2=0可变形为(
)2-(
)-1=0,根据p2-p-1=0和(
)2-(
)-1=0的特征.
∴p、
是方程x2-x-1=0的两个不相等的实数根,则p+
=1,即
=1.
根据阅读材料所提供的方法,完成下面的解答.
已知:2m2-5m-1=0,
+
-2=0且m≠n,求下列各式的值:(1)
+
;(2)(m-n)2.
| pq+1 |
| q |
解:由p2-p-1=0,及1-q-q2=0可知p≠0,q≠0又∵pq≠1,∴p≠
| 1 |
| q |
∵1-q-q2=0可变形为(
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
∴p、
| 1 |
| q |
| 1 |
| q |
| pq+1 |
| q |
根据阅读材料所提供的方法,完成下面的解答.
已知:2m2-5m-1=0,
| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
分析:由
+
-2=0得到2n2-5n-1=0,根据题目所给的方法得到m、n是方程2x2-5x-1=0的两个不相等的实数根,根据根与系数的关系得到m+n=
,mn=-
,
(1)通分得到原式=
,然后利用整体代入的方法计算;
(2)利用完全平方公式变形得到原式=(m+n)2-4mn,然后利用整体代入的方法计算.
| 1 |
| n2 |
| 5 |
| n |
| 5 |
| 2 |
| 1 |
| 2 |
(1)通分得到原式=
| m+n |
| mn |
(2)利用完全平方公式变形得到原式=(m+n)2-4mn,然后利用整体代入的方法计算.
解答:解:∵
+
-2=0,
∴2n2-5n-1=0,
根据2m2-5m-1=0和2n2-5n-1=0的特征,
∴m、n是方程2x2-5x-1=0的两个不相等的实数根,
∴m+n=
,mn=-
,
(1)原式=
=
=-5;
(2)原式=(m+n)2-4mn=(
)2-4×(-
)=
.
| 1 |
| n2 |
| 5 |
| n |
∴2n2-5n-1=0,
根据2m2-5m-1=0和2n2-5n-1=0的特征,
∴m、n是方程2x2-5x-1=0的两个不相等的实数根,
∴m+n=
| 5 |
| 2 |
| 1 |
| 2 |
(1)原式=
| m+n |
| mn |
| ||
-
|
(2)原式=(m+n)2-4mn=(
| 5 |
| 2 |
| 1 |
| 2 |
| 33 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
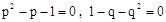 且
且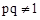 ,求
,求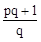 的值.
的值.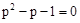 ,及
,及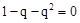 可知
可知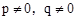 ,又∵
,又∵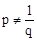 .
.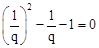 ,根据
,根据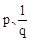 是方程
是方程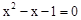 的两个不相等的实数根,则
的两个不相等的实数根,则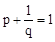 ,即
,即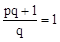 .
.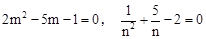 ,且
,且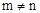 ,求下列各式的值(1)
,求下列各式的值(1)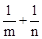 ;(2)
;(2)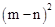 .
. 的值.
的值. .
. +
+ -2=0且m≠n,求下列各式的值:(1)
-2=0且m≠n,求下列各式的值:(1) +
+ ;(2)(m-n)2.
;(2)(m-n)2.