题目内容
(1)新人教版初中数学教材中我们学习了:若关于x的一元二次方程ax2+bx+c=0的两根为x1,x2,则x1+x2=-| b |
| a |
| c |
| a |
请你完成以上的填空.
(2)阅读材料:已知m2-m-1=0,n2+n-1=0,且mn≠1.求
| mn+1 |
| n |
解:由n2+n-1=0可知n≠0.
∴1+
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n2 |
| 1 |
| n |
又m2-m-1=0,且mn≠1,即m≠
| 1 |
| n |
∴m,
| 1 |
| n |
| 1 |
| n |
| mn+1 |
| n |
(3)根据阅读材料所提供的方法及(1)的方法完成下题的解答.
已知2m2-3m-1=0,n2+3n-2=0,且mn≠1.求m2+
| 1 |
| n2 |
分析:(1)根据根与系数的关系可求出x1+x2和x1x2的值,然后再代值求解即可.
(2)根据(2)的解法可求出m+
和m•
的值,然后将m和
看作一个整体,根据(1)的方法进行化简;然后再代值求解.
(2)根据(2)的解法可求出m+
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
解答:解:(1)2,-1,(2分)6;(4分)
(3)由n2+3n-2=0可知n≠0;
∴1+
-
=0;(5分)
∴
-
-1=0(6分)
又2m2-3m-1=0,且mn≠1,即m≠
;(7分)
∴m、
是方程2x2-3x-1=0的两根,(8分)
∴m+
=
,m•
=-
;(10分)
∴m2+
=(m+
)2-2m•
=(
)2-2•(-
)=
.(12分)
(3)由n2+3n-2=0可知n≠0;
∴1+
| 3 |
| n |
| 2 |
| n2 |
∴
| 2 |
| n2 |
| 3 |
| n |
又2m2-3m-1=0,且mn≠1,即m≠
| 1 |
| n |
∴m、
| 1 |
| n |
∴m+
| 1 |
| n |
| 3 |
| 2 |
| 1 |
| n |
| 1 |
| 2 |
∴m2+
| 1 |
| n2 |
| 1 |
| n |
| 1 |
| n |
| 3 |
| 2 |
| 1 |
| 2 |
| 13 |
| 4 |
点评:能够正确的理解材料的含义,并熟练地掌握根与系数的关系是解答此题的关键.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
若运用湘教版初中数学教材上使用的某种电子计算器进行计算,则按键 的显示结果是( )
的显示结果是( )
 的显示结果是( )
的显示结果是( )| A、15 | B、±15 | C、-15 | D、25 |
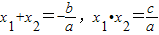 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.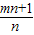 的值.
的值.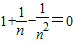 .∴
.∴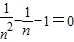
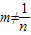 .
.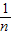 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴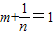 .∴
.∴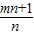 =1.
=1.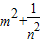 的值.
的值.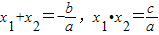 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.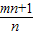 的值.
的值.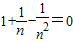 .∴
.∴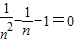
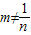 .
.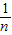 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴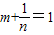 .∴
.∴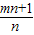 =1.
=1.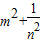 的值.
的值.