题目内容
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 的延长线上,
的延长线上,![]() .
.
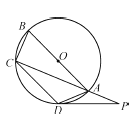
(Ⅰ)若![]() ,求弧
,求弧![]() 的长;
的长;
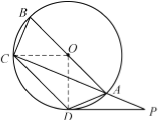
(Ⅱ)若弧![]() 弧
弧![]() ,
,![]() ,求证:
,求证:![]() 是
是![]() 的切线.
的切线.
【答案】(Ⅰ)![]() 的长 =π;(Ⅱ)证明见解析.
的长 =π;(Ⅱ)证明见解析.
【解析】
试题分析:(Ⅰ)连接OC,OD,由圆周角定理可得∠COD=90°,然后利用弧长公式即可得;
(Ⅱ)由![]() =
=![]() ,可得∠BOC=∠AOD,从而可得∠AOD=45°,再由三角形内角和从而可得∠ODA=67.5°,由AD=AP可得∠ADP=∠APD,由∠CAD=∠ADP+∠APD,∠CAD=45°可得∠ADP=22.5°,继而可得∠ODP=90°,从而得 PD是⊙O的切线.
,可得∠BOC=∠AOD,从而可得∠AOD=45°,再由三角形内角和从而可得∠ODA=67.5°,由AD=AP可得∠ADP=∠APD,由∠CAD=∠ADP+∠APD,∠CAD=45°可得∠ADP=22.5°,继而可得∠ODP=90°,从而得 PD是⊙O的切线.
试题解析:(Ⅰ)连接OC,OD,∵∠COD=2∠CAD,∠CAD=45°,∴∠COD=90°,∵AB=4,∴OC=![]() AB=2,∴
AB=2,∴![]() 的长=
的长=![]() =π;
=π;
(Ⅱ)∵![]() =
=![]() ,∴∠BOC=∠AOD,∵∠COD=90°,∴∠AOD=
,∴∠BOC=∠AOD,∵∠COD=90°,∴∠AOD=![]() =45°,∵OA=OD,∴∠ODA=∠OAD,∵∠AOD+∠ODA+∠OAD=180°,∴∠ODA=
=45°,∵OA=OD,∴∠ODA=∠OAD,∵∠AOD+∠ODA+∠OAD=180°,∴∠ODA=![]() =67.5°,∵AD=AP,∴∠ADP=∠APD,∵∠CAD=∠ADP+∠APD,∠CAD=45°,∴∠ADP=
=67.5°,∵AD=AP,∴∠ADP=∠APD,∵∠CAD=∠ADP+∠APD,∠CAD=45°,∴∠ADP=![]() ∠CAD=22.5°,∴∠ODP=∠ODA+∠ADP=90°,又∵OD是半径,∴PD是⊙O的切线.
∠CAD=22.5°,∴∠ODP=∠ODA+∠ADP=90°,又∵OD是半径,∴PD是⊙O的切线.

练习册系列答案
相关题目