题目内容
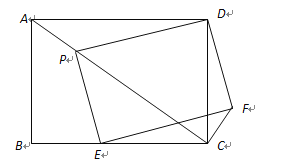
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 分别是线段AC、BC上的点,且四边形
分别是线段AC、BC上的点,且四边形![]() 为矩形.
为矩形.
(Ⅰ)若![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)AP的长为4或5或![]() ;(Ⅱ)CF=
;(Ⅱ)CF=![]()
【解析】
试题分析:(Ⅰ)分情况CP=CD、PD=PC、DP=DC讨论即可得;
(Ⅱ)连结PF、DE,记PF与DE的交点为O,连结OC,通过证明△ADP∽△CDF,从而得![]() ,由AP=
,由AP=![]() ,从而可得CF=
,从而可得CF=![]() .
.
试题解析:(Ⅰ)在矩形ABCD中,AB=6,AD=8,∠ADC=90°,∴DC=AB=6, AC=![]() =10;
=10;
要使△PCD是等腰三角形,有如下三种情况:
(1)当CP=CD时,CP=6,∴AP=AC-CP=4 ;
(2)当PD=PC时,∠PDC=∠PCD,∵∠PCD+∠PAD=∠PDC+∠PDA=90°,∴∠PAD=∠PDA,∴PD=PA,∴PA=PC,∴AP=![]() ,即AP=5;
,即AP=5;
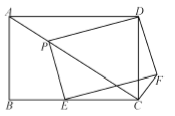
(3)当DP=DC时,过D作DQ⊥AC于Q,则PQ=CQ,∵S△ADC=![]() AD·DC=
AD·DC=![]() AC·DQ,∴DQ=
AC·DQ,∴DQ=![]() ,∴CQ=
,∴CQ=![]() ,∴PC=2CQ =
,∴PC=2CQ =![]() ,∴AP=AC-PC=
,∴AP=AC-PC=![]() .
.
综上所述,若△PCD是等腰三角形,AP的长为4或5或![]() ;
;
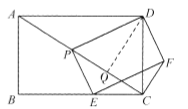
(Ⅱ)连结PF、DE,记PF与DE的交点为O,连结OC,
∵四边形ABCD和PEFD都是矩形,∴∠ADC=∠PDF=90°,即∠ADP+∠PDC=∠PDC+∠CDF,∴∠ADP=∠CDF,∵∠BCD=90°,OE=OD,∴OC=![]() ED,在矩形PEFD中,PF=DE,∴OC=
ED,在矩形PEFD中,PF=DE,∴OC=![]() PF,∵OP=OF=
PF,∵OP=OF=![]() PF,∴OC=OP=OF,∴∠OCF=∠OFC,∠OCP=∠OPC,又∵∠OPC+∠OFC+∠PCF=180°,∴2∠OCP+2∠OCF=180°,∴∠PCF=90°,即∠PCD+∠FCD=90°,在Rt△ADC中,∠PCD+∠PAD=90°,∴∠PAD=∠FCD,∴△ADP∽△CDF,∴
PF,∴OC=OP=OF,∴∠OCF=∠OFC,∠OCP=∠OPC,又∵∠OPC+∠OFC+∠PCF=180°,∴2∠OCP+2∠OCF=180°,∴∠PCF=90°,即∠PCD+∠FCD=90°,在Rt△ADC中,∠PCD+∠PAD=90°,∴∠PAD=∠FCD,∴△ADP∽△CDF,∴![]() ,∵AP=
,∵AP=![]() ,∴CF=
,∴CF=![]() .
.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案