Question

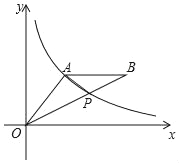
【题目】在△ABC中，D是BC上一点，且BD＝2DC，E是AD的中点，旋转过E点的直线l．

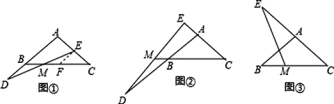
（1）如图1，当l经过C，交AB于G，求证：BG＝3AG；

（2）如图2，当l平分△ABC的面积，分别交BC，AC于M，N，求的值；

（3）若AB＝8，AC＝6，BC＝12，且l平分△ABC的周长，分别交BC，AD于M，N，直接写出BM的长．

Answer 1

【答案】（1）见解析；（2）=；（3）BM＝.

【解析】

（1）过点A作BC的平行线AF，利用点E是AD中点构造△AEF≌△DEC，得到AF＝CD，即BC＝3AF．又由平行得△AFG∽△BCG，即得到BG与AG的比即为相似比等于BC与AF的比，得证．

（2）连接CE与BE，由AE＝DE可得等底同高的△AEC与△DEC面积相等；由BD＝2DC可得同高的△ABD与△ACD面积有2倍关系．故可设这最小的两个△AEN与△CEN的面积分别为a和b，用a和b表示图中所有三角形面积．过点A作BC平行线AG，构造△AEH≌△DEM与△ANH∽△CNM，根据面积比求得△ANH与△CNM的相似比，进而求得a与b的关系．而可看作同高的△BME与△CME的面积比，根据a与b的关系即能求得．

（3）构造△AEH≌△DEM与△ANH∽△CNM，设AH＝DM＝x，用x表示△ABC三边上的线段，再利用△ANH∽△CNM的对应边成比例列得关于x的方程，求出x即求得BM的长．

解：（1）证明：过点A作AF∥BC，交CG延长线与点F

∴∠F＝∠DCE

∵点E是AD中点

∴AE＝DE

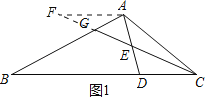
在△AEF与△DEC中

，

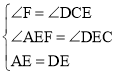∴△AEF≌△DEC（AAS）

∴AF＝CD

∵BD＝2DC

∴BC＝BD+DC＝3DC＝3AF

∵AF∥BC

∴△AFG∽△BCG

∴

∴BG＝3AG

（2）过点A作AH∥BC，交直线MN与点H，连接BE、CE

∴∠H＝∠DME

∵点E是AD中点

∴AE＝DE

在△AEH与△DEM中

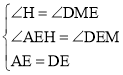
∴△AEH≌△DEM（AAS）

∴S△AEH＝S△DEM

设S△AEN＝a，S△CEN＝b

∴S△AEC＝S△AEN+S△CEN＝a+b

∴S△DEC＝S△AEC＝a+b，S△DEB＝S△AEB

∴S△ACD＝S△DEC+S△AEC＝2a+2b

∵BD＝2DC

∴S△ABD＝2S△ACD＝4a+4b

∴S△DEB＝S△AEB＝S△ABD＝2a+2b，S△ABC＝S△ABD+S△ACD＝6a+6b

∵直线MN平分S△ABC

∴S四边形ABMN＝S△CMN＝S△ABC＝3a+3b

∴S△BEM＝S四边形ABMN﹣S△ABE﹣S△AEN＝3a+3b﹣（2a+2b）﹣a＝b，S△DEM＝S△CMN﹣S△DEC﹣S△CEN＝3a+3b﹣（a+b）﹣b＝2a+b

∴S△AEH＝S△DEM＝2a+b

∴S△ANH＝S△AEH﹣S△AEN＝2a+b﹣a＝a+b

∵AH∥BC

∴△ANH∽△CNM

∴

∴

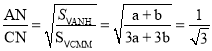
即a

∴，

∴的值为；

（3）过点A作AH∥BC，交直线MN与点H，

由（2）得：△AEH≌△DEM，△ANH∽△CNM

∴设AH＝DM＝x

∵BC＝12，BD＝2DC

∴DC＝4，BD＝8

∴BM＝BD﹣MD＝8﹣x，CM＝DC+MD＝4+x

∵直线MN平分△ABC周长，AB＝8，AC＝6

∴MD+DC+CN＝AN+AB+BM＝（AB+AC+BC）＝13

∴CN＝13﹣MD﹣CD＝13﹣x﹣4＝9﹣x，AN＝13﹣AB﹣BM＝13﹣8﹣（8﹣x）＝x﹣3

∵△ANH∽△CNM

∴

∴

解得：x1＝，x2＝（舍去）

∴BM