题目内容
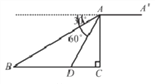
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(0,8),(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A'处,折痕所在直线交y轴正半轴于点C.

(1)求直线BC的函数表达式;
(2)把直线BC向左平移,使之经过点A',求平移后直线的函数表达式.
【答案】(1)y=﹣![]() x+3;(2)y=﹣
x+3;(2)y=﹣![]() x﹣2.
x﹣2.
【解析】
(1)在Rt△OAB中,OA=8,OB=6,用勾股定理计算出AB=10,再根据折叠的性质得BA′=BA=10,CA′=CA,则OA′=BA′﹣OB=4,设OC=t,则CA=CA′=8﹣t,在Rt△OA′C中,根据勾股定理得到t2+42=(8﹣t)2,解得t=3,则C点坐标为(0,3),然后利用待定系数法确定直线BC的函数表达式即可;
(2)由(1)可知点A′的坐标为(﹣4,0),根据平移的性质可设平移后的直线为y=﹣![]() x+m,再将(﹣4,0)代入即可求得平移后直线的函数表达式.
x+m,再将(﹣4,0)代入即可求得平移后直线的函数表达式.
解:(1)∵A(0,8),B(6,0),
∴OA=8,OB=6,
在Rt△OAB中,AB=![]() =10.
=10.
∵△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,
∴BA′=BA=10,CA′=CA,
∴OA′=BA′﹣OB=10﹣6=4.
设OC=t,则CA=CA′=8﹣t,
在Rt△OA′C中,∵OC2+OA′2=CA′2,
∴t2+42=(8﹣t)2,解得t=3,
∴C点坐标为(0,3),
设直线BC的解析式为y=kx+b,
把B(6,0)、C(0,3)代入
得![]() ,解得
,解得 ,
,
∴直线BC的解析式为y=﹣![]() x+3;
x+3;
(2)∵OA′=4,
∴点A′的坐标为(﹣4,0)
∵把直线BC向左平移,使之经过点A',
∴设平移后直线的函数表达式为y=﹣![]() x+m,
x+m,
将(﹣4,0)代入,得
0=2+m,
解得m=﹣2,
∴平移后直线的函数表达式为y=﹣![]() x﹣2.
x﹣2.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】探究函数![]() 的图象与性质,下面是探究过程,请补充完整:
的图象与性质,下面是探究过程,请补充完整:
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
函数![]() 的自变量
的自变量![]() 的取值范围是__________,
的取值范围是__________, ![]() 的值为__________.
的值为__________.
(![]() )描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
)描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
(![]() )进一步探究函数图象发现:
)进一步探究函数图象发现:
①函数图象与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有__________个实数根.
有__________个实数根.
②方程![]() 有__________个实数根.
有__________个实数根.
③结合函数的图象,写出该函数的一条性质__________.