Question

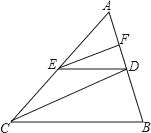
【题目】如图，在△ABC中，EF∥CD，DE∥BC．

（1）求证：AF：FD=AD：DB；

（2）若AB=15，AD：BD=2：1，求DF的长．

Answer 1

【答案】（1）详见解析；（2）.

【解析】试题分析：（1）根据平行线分线段成比例定理证得，，由此即可证得结论；（2）由AB=15，AD：BD=2：1，即可得AD=10，再由AF：FD=AD：DB得到AF：FD=2：1，所以AF=2DF，又因AF+DF=10，即可得2DF+DF=10，所以DF=．

试题解析：

（1）证明：∵EF∥CD，

∴，

∵DE∥BC，

∴

∴．

（2）∵AD：BD=2：1，

∴BD=AD，

∴AD+AD=15，

∴AD=10，

∵AF：FD=AD：DB，

∴AF：FD=2：1，

∴AF=2DF，

∵AF+DF=10，

∴2DF+DF=10，

∴DF=．