题目内容
如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
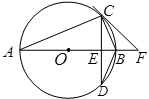
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.

(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
(1)证明见解析;(2)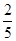 .
.
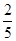 .
.试题分析:(1)连接OC,由OA=OA可知∠ACO=∠A,再根据∠FCB=∠A可知∠ACO=∠FCB,由于AB是⊙O的直径,所以∠ACO+∠OCB=90°故∠FCB+∠OCB=90°故可得出结论;
(2)由AB是⊙O的直径,CD⊥AB可知
试题解析:(1)连接OC,
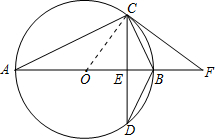
∵OA=OC,
∴∠ACO=∠A,
又∵∠FCB=∠A
∴∠ACO=∠FCB,
又∵AB是⊙O的直径
∴∠ACO+∠OCB=90°,∠FCB+∠OCB=90°
∴直线CF为⊙O的切线,
(2)∵AB是⊙O 直径
∴∠ACB=90°
∵DC⊥AB
∴
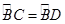
∴BC=BD,∠A=∠D
∴
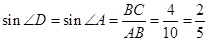
考点: 1.切线的判定;2.圆周角定理;3.解直角三角形.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 =2、
=2、 =4,若⊙O1与⊙O2的圆心距
=4,若⊙O1与⊙O2的圆心距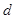 =5.则⊙O1与⊙O2的位置关系是___________.
=5.则⊙O1与⊙O2的位置关系是___________. 的半径为3cm,
的半径为3cm,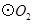 的半径为4cm,两圆的圆心距
的半径为4cm,两圆的圆心距 为7cm,则
为7cm,则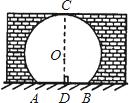
 AD,则∠DBC的度数为
AD,则∠DBC的度数为 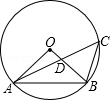
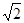
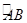 =
=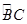 ,∠AOB=60°,则∠BDC的度数是( )
,∠AOB=60°,则∠BDC的度数是( )