题目内容
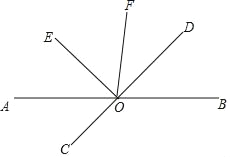
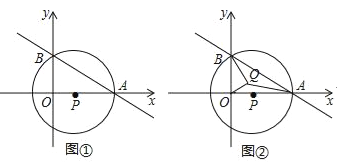
【题目】如图①,在平面直角坐标系中,直线y=kx+b与x轴正半轴交于点A,与y轴负半轴交于点B,圆心P在x轴的正半轴上,已知AB=10,AP=![]()
(1)求点P到直线AB的距离;
(2)求直线y=kx+b的解析式;
(3)在图②中存在点Q,使得∠BQO=90°,连接AQ,请求出AQ的最小值.
【答案】(1)![]() (2)y=﹣
(2)y=﹣![]() x+6(3)
x+6(3)![]()
【解析】
(1)先根据垂径定理求出得出AD=5,最后用勾股定理即可得出结论;(2)设出OP=x,利用勾股定理即可得出OP的值,最后用待定系数法即可得出结论;(3)先确定出AQ取得最小值时的条件,最后用勾股定理即可得出结论.
(1)如图①,过点P作PD⊥AB于D,由垂径定理得AD=DB=![]() AB=5
AB=5
在Rt△APD中,由AD=5,AP=![]() ,
,
根据勾股定理得,得PD2+AD2=AP2
则PD=![]() ,
,
∴点P到直线AB的距离为![]() ;
;
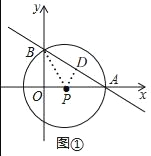
(2)连接BP,设OP=x
∵OB2=BP2﹣OP2,OB2=AB2﹣OA2
∴OB2=(![]() )2﹣x2,OB2=102﹣(
)2﹣x2,OB2=102﹣(![]() +x)2
+x)2
∴(![]() )2﹣x2=102﹣(
)2﹣x2=102﹣(![]() +x)2
+x)2
解得:x=![]() ,
,
∴OA=8,OB=6,
∴A(8,0),B(0,6),
∴![]() ,
,
∴ ,
,
∴直线AB的解析式为y=﹣![]() x+6;
x+6;
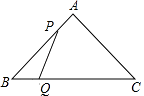
(3)解:如图②,∵∠OQB=90°,
∴点Q是以OB为直径的圆上,
以OB为直径作圆E,连接EQ,AE,
∴EQ+AQ≥AE
当点A,Q,E三点在一直线上时,AQ有最小值,
在Rt△AOE中,AE=![]() ,
,
∴AQ的最小值为AE﹣OE=![]() ﹣3.
﹣3.

 阅读快车系列答案
阅读快车系列答案【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁): 39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
总 计 | 50 |
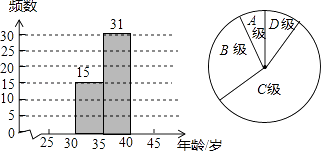
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.