题目内容
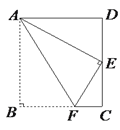
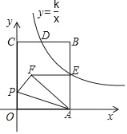
【题目】如图,将矩形OABC置于一平面直角坐标系中,顶点A,C分别位于x轴,y轴的正半轴上,点B的坐标为(5,6),双曲线y=![]() (k≠0)在第一象限中的图象经过BC的中点D,与AB交于点E,P为y轴正半轴上一动点,把△OAP沿直线AP翻折,使点O落在点F处,连接FE,若FE∥x轴,则点P的坐标为___.
(k≠0)在第一象限中的图象经过BC的中点D,与AB交于点E,P为y轴正半轴上一动点,把△OAP沿直线AP翻折,使点O落在点F处,连接FE,若FE∥x轴,则点P的坐标为___.
【答案】(0,![]() )或(0,15).
)或(0,15).
【解析】
延长EF交CO于G,依据反比例函数图象上点的坐标特征,即可得到点E的横坐标为5,点E的纵坐标为3,再根据勾股定理可得EF的长,设OP=x,则PG=3﹣x,分两种情况讨论,依据Rt△FGP中,FG2+PG2=PF2,即可得到x的值,进而得出点P的坐标.
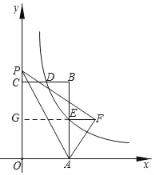
如图所示,延长EF交CO于G,
∵EF∥x轴,
∴∠FGP=90°=∠AEF,
∵双曲线y=![]() (k≠0)经过矩形OABC的边BC的中点D,点B的坐标为(5,6),
(k≠0)经过矩形OABC的边BC的中点D,点B的坐标为(5,6),
∴点D(![]() ,6),
,6),
∴k=15,
又∵点E的横坐标为5,
∴点E的纵坐标为![]() =3,即AE=3,
=3,即AE=3,
①当点F在AB左侧时,由折叠可得,AF=AO=5,
∴Rt△AEF中,EF=![]() =4,
=4,
∴GF=5﹣4=1,
设OP=x,则PG=3﹣x,
∵Rt△FGP中,FG2+PG2=PF2,
∴12+(3﹣x)2=x2,
解得x=![]() ,
,
∴点P的坐标为(0,![]() );
);
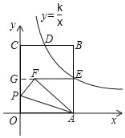
②当点F在AB右侧时,同理可得EF=4,
∴GF=5+4=9,
设OP=x,则PG=x﹣3,
∵Rt△FGP中,FG2+PG2=PF2,
∴92+(x﹣3)2=x2,
解得x=15,
∴点P的坐标为(0,15);
故答案为:(0,![]() )或(0,15).
)或(0,15).

练习册系列答案
相关题目