题目内容
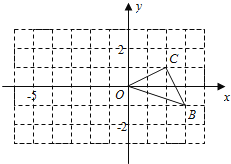
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,点
,点![]() 在线段
在线段![]() 上,以
上,以![]() 为直径的⊙D经过点
为直径的⊙D经过点![]() .
.
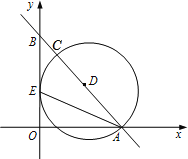
(1)判断⊙D与![]() 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)求点![]() 的坐标.
的坐标.
【答案】(1)相切,理由见解析;(2)C(![]() ,6).
,6).
【解析】
(1)本题须先作出辅助线连接ED,再证出ED⊥OB即可.
(2)本题须设点C的坐标为(m,n),再解直角三角形得出m、n的值即可求出结果.
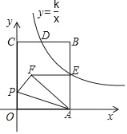
解:(1)相切,连接ED,
∵∠OAB的平分线交y轴于点E,
∴∠DAE=∠EAO.
∵∠DEA=∠DAE,
∴∠DEA=∠DAE=∠EAO,
所以ED∥OA,
所以ED⊥OB;
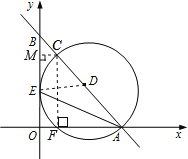
(2)作CM⊥BO,CF⊥AO,
易得AB=10.设C(m,n),ED=R,
则DE⊥BO,
∴ED∥AO,
△BED∽△BOA,
![]()
![]()
解得:R=![]() ,
,
∴△AFC∽△AOB,
∴![]()
∴![]()
解得:CF=6,
利用勾股定理可求出AF=4.5,
∴OF=1.5,
所以C(![]() ,6).
,6).

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目