题目内容
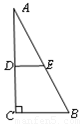
 如图,梯形纸片ABCD中,AD∥BC,CD⊥BC,将其沿对角线BD折叠,点A恰好落在DC上,记为点A′,若AD=7,AB=13,则S梯形ABCD=
如图,梯形纸片ABCD中,AD∥BC,CD⊥BC,将其沿对角线BD折叠,点A恰好落在DC上,记为点A′,若AD=7,AB=13,则S梯形ABCD=
- A.94
- B.104
- C.114
- D.124
C
分析:由于AD∥BC,CD⊥BC,可知∠ADC=∠C=90°,∠2=∠3,于是∠1+∠2=90°,根据翻折变换的性质可知∠1=∠2,进而可求∠3=∠2=∠1=45°,从而可知BC=CD,再设A′C=x,那么BC=CD=x+7,在Rt△A′BC中利用勾股定理可求A′C=5,再结合梯形面积公式易求其面积.
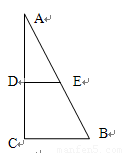
解答: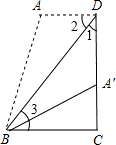 解:如右图所示,
解:如右图所示,
∵AD∥BC,CD⊥BC,
∴∠ADC=∠C=90°,∠2=∠3,
即∠1+∠2=90°,
又∵△BA′D≌△BAD,
∴∠1=∠2,A′D=AD=7,
∴∠1=∠2=45°,
∴∠1=∠3=45°,
∴BC=CD,
设A′C=x,那么BC=CD=x+7,
在Rt△A′BC中,A′B2=BC2+A′C2,
即x2+(x+7)2=132,
解得x=5,x=-12(负数,舍去),
∴A′C=5,BC=12,
∴S梯形ABCD= (7+12)×12=114.
(7+12)×12=114.
故选C.
点评:本题考查了翻折变换、全等三角形的性质、勾股定理,解题的关键是注意一个图形翻折后所得图形与原图形全等.
分析:由于AD∥BC,CD⊥BC,可知∠ADC=∠C=90°,∠2=∠3,于是∠1+∠2=90°,根据翻折变换的性质可知∠1=∠2,进而可求∠3=∠2=∠1=45°,从而可知BC=CD,再设A′C=x,那么BC=CD=x+7,在Rt△A′BC中利用勾股定理可求A′C=5,再结合梯形面积公式易求其面积.
解答:
 解:如右图所示,
解:如右图所示,∵AD∥BC,CD⊥BC,
∴∠ADC=∠C=90°,∠2=∠3,
即∠1+∠2=90°,
又∵△BA′D≌△BAD,
∴∠1=∠2,A′D=AD=7,
∴∠1=∠2=45°,
∴∠1=∠3=45°,
∴BC=CD,
设A′C=x,那么BC=CD=x+7,
在Rt△A′BC中,A′B2=BC2+A′C2,
即x2+(x+7)2=132,
解得x=5,x=-12(负数,舍去),
∴A′C=5,BC=12,
∴S梯形ABCD=
 (7+12)×12=114.
(7+12)×12=114.故选C.
点评:本题考查了翻折变换、全等三角形的性质、勾股定理,解题的关键是注意一个图形翻折后所得图形与原图形全等.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
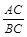 的值是 .
的值是 .