题目内容
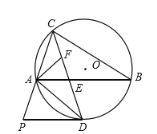
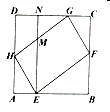
【题目】如图,已知![]() 中,
中,![]() ,D是线段AC上一点(不与A,C重合),连接BD,将
,D是线段AC上一点(不与A,C重合),连接BD,将![]() 沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F,若
沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F,若![]() 是直角三角形,则AF的长为_________.
是直角三角形,则AF的长为_________.

【答案】![]() 或
或![]()
【解析】
分别讨论∠E=90°,∠EBF=90°两种情况:①当∠E=90°时,由折叠性质和等腰三角形的性质可推出△BDC为等腰直角三角形,再求出∠ABD=∠ABE=22.5°,进而得到∠F=45°,推出△ADF为等腰直角三角形即可求出斜边AF的长度;②当∠EBF=90°时,先证△ABD∽△ACB,利用对应边成比例求出AD和CD的长,再证△ADF∽△CDB,利用对应边成比例求出AF.
①当∠E=90°时,由折叠性质可知∠ADB=∠E=90°,如图所示,
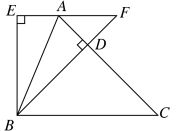
在△ABC中,CA=CB=4,∠C=45°
∴∠ABC=∠BAC=![]() =67.5°
=67.5°
∵∠BDC=90°,∠C=45°
∴△BCD为等腰直角三角形,
∴CD=![]() BC=
BC=![]() ,∠DBC=45°
,∠DBC=45°
∴∠EBA=∠DBA=∠ABC-∠DBC=67.5°-45°=22.5°
∴∠EBF=45°
∴∠F=90°-45°=45°
∴△ADF为等腰直角三角形
∴AF=![]()
②当∠EBF=90°时,如图所示,
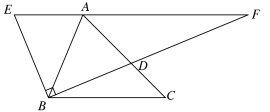
由折叠的性质可知∠ABE=∠ABD=45°,
∵∠BAD=∠CAB
∴△ABD∽△ACB
∴![]()
由情况①中的AD=![]() ,BD=
,BD=![]() ,
,
可得AB=![]()
∴AD=![]()
∴CD=![]()
∵∠DBC=∠ABC-∠ABD=22.8°
∵∠E=∠ADB=∠C+∠DBC=67.5°
∴∠F=22.5°=∠DBC
∴EF∥BC
∴△ADF∽△CDB
∴![]()
∴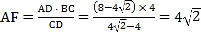
∵∠E=∠BDA=∠C+∠DBC=45°+67.5°-∠ABD=112.5°-∠ABD,∠EBF=2∠ABD
∴∠E+∠EBF=112.5°+∠ABD>90°
∴∠F不可能为直角
综上所述,AF的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案