题目内容
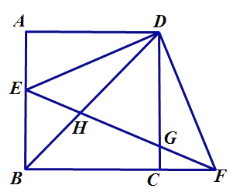
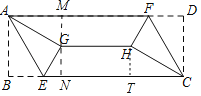
【题目】如图,在矩形ABCD中,AB=2![]() ,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )
,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )

A.3B.4C.5D.7
【答案】B
【解析】
如图作GM⊥AD于M交BC于N,作HT⊥BC于T.通过解直角三角形求出AM、GM的长,同理可得HT、CT的长,再通过证四边形ABNM为矩形得MN=AB=2![]() ,BN=AM=3,最后证四边形GHTN为平行四边形可得GH=TN即可解决问题.
,BN=AM=3,最后证四边形GHTN为平行四边形可得GH=TN即可解决问题.
解:如图作GM⊥AD于M交BC于N,作HT⊥BC于T.
∵△ABE沿着AE翻折后得到△AGE,
∴∠GAM=∠BAE,AB=AG=2![]() ,
,
∵AG分别平分∠EAD,
∴∠BAE=∠EAG,
∵∠BAD=90°,
∴∠GAM=∠BAE=∠EAG=30°,
∵GM⊥AD,
∴∠AMG=90°,
∴在Rt△AGM中,sin∠GAM=![]() ,cos∠GAM=
,cos∠GAM=![]() ,
,
∴GM=AGsin30°=![]() ,AM=AGcos30°=3,
,AM=AGcos30°=3,
同理可得HT=![]() ,CT=3,
,CT=3,
∵∠AMG=∠B=∠BAD=90°,
∴四边形ABNM为矩形,
∴MN=AB=2![]() ,BN=AM=3,
,BN=AM=3,
∴GN=MN﹣GM=![]() ,
,
∴GN=HT,
又∵GN∥HT,
∴四边形GHTN是平行四边形,
∴GH=TN=BC﹣BN﹣CT=10﹣3﹣3=4,
故选:B.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目