题目内容
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
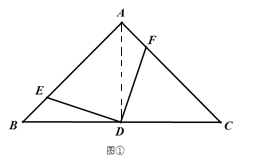
(1)观察猜想:如图①,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() 于点
于点![]() ,则线段
,则线段![]() 与
与![]() 的数量关系是_______;(不说明理由)
的数量关系是_______;(不说明理由)
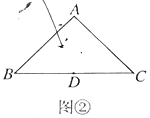
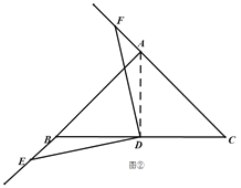
(2)类比探究:若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() 于点
于点![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,在图②中画出符合题意的图形,并说明理由;
的数量关系,在图②中画出符合题意的图形,并说明理由;
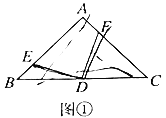
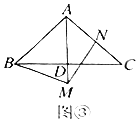
(3)解决问题:如图③,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.(直接写出结果,不说明理由.)
的长.(直接写出结果,不说明理由.)
【答案】(1)BE=AF;(2)BE=AF,理由见解析;(3)![]() .
.
【解析】
(1)连接AD,根据等腰三角形的性质可得出AD=BD、∠EBD=∠FAD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△BDE≌△ADF(ASA),再根据全等三角形的性质即可证出BE=AF;
(2)连接AD,根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD、BD=AD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△EDB≌△FDA(ASA),再根据全等三角形的性质即可得出BE=AF;
(3)过点M作MG∥BC,交AB的延长线于点G,同理证明△BMG≌△NMA,得到AN=GB=1,再根据等腰直角三角形求出AG的长,即可求解.
(1)证明:连接AD,如图①所示.
∵∠A=90°,AB=AC,
∴△ABC为等腰直角三角形,∠EBD=45°.
∵点D为BC的中点,
∴AD=![]() BC=BD,∠FAD=45°.
BC=BD,∠FAD=45°.
∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,
∴∠BDE=∠ADF.
在△BDE和△ADF中,
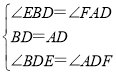 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF.
(2)BE=AF
理由:如图②,连结AD,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠C=![]() (180°-∠BAC)=
(180°-∠BAC)=![]() (180°-90°)=45°
(180°-90°)=45°
∵BD=AD,AB=AC,
∴AD⊥BC,
∴∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() ×90°=45°,
×90°=45°,
∴∠BAD=∠ABC,
∴AD=BD
又∠CAD=∠ABC=45°,
∴∠DAF=∠DBE=135°
∵DE⊥DF,
∴∠BDE+∠BDF=90°
又AD⊥BC,
∴∠ADF+∠BDF=90°,
∴∠BDE=∠ADF
在△BDE和△ADF中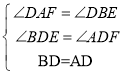 ,
,
∴△BDE≌△ADF,
∴BE=AF
(3)如图③,过点M作MG∥BC,交AB的延长线于点G,
∵DA⊥BC,
∴AM⊥GM,
故△AMG为等腰直角三角形
∴GM=AM=2,故AG=2![]()
∵![]()
同(1)理可得△BMG≌△NMA,
∴AN=GB=1,
∴![]() =AG-BG=AG-AN=
=AG-BG=AG-AN=![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案