题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() ,
,![]() 移动的速度相同,
移动的速度相同,![]() 与
与![]() 相交于点
相交于点![]() .
.
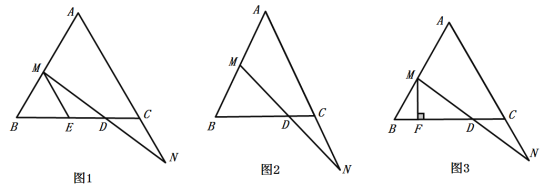
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() ,当点
,当点![]() 移动到
移动到![]() 的中点时,求
的中点时,求![]() 的长度;
的长度;
(3)如图3,过点![]() 作
作![]() 于点
于点![]() .在点
.在点![]() 从点
从点![]() 向点
向点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)移动的过程中,线段
重合)移动的过程中,线段![]() 与
与![]() 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出![]() 与
与![]() 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由.
【答案】(1)证明见解析;(2)![]() 的长度为
的长度为![]() ;(3)
;(3)![]() 与
与![]() 的长度和保持不变,和为4.
的长度和保持不变,和为4.
【解析】
(1)由平行的性质和等腰三角形的性质进行等边和等角转换,即可判定![]() ;
;
(2)由(1)的结论和等边三角形的性质,通过等量转换即可得解;
(3)首先过点![]() 作
作![]() ,由等腰三角形的性质以及全等三角形的性质,即可求得
,由等腰三角形的性质以及全等三角形的性质,即可求得![]() 与
与![]() 的长度保持不变.
的长度保持不变.
(1)∵点![]() ,
,![]() 同时移动且移动的速度相同,
同时移动且移动的速度相同,
![]() ,
,
![]() ,
,
![]()
又![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 与
与![]() 相交于点
相交于点![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,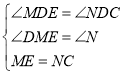 ,
,
![]() (AAS);
(AAS);
(2)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图所示:
,如图所示:

![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]()
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() .
.
由(1)易得![]() ,
,
![]() ,
,
![]() ,
,
![]() 的长度为
的长度为![]() ;
;
(3)保持不变;
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图所示:
,如图所示:
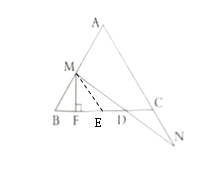
由(1)易得![]() ,
,![]() ,
,
![]() ,
,![]() 是等腰三角形.
是等腰三角形.
![]() ,
,
![]() 是
是![]() 的中线,
的中线,
![]() ,
,
![]() ,
,
![]() 与
与![]() 的长度和保持不变.
的长度和保持不变.

练习册系列答案
相关题目