题目内容
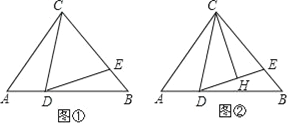
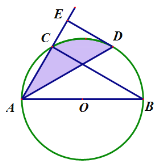
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AD=BC,⊙O半径为6,求∠CAD与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
【答案】(1)直线DE与⊙O相切,理由见解析;(2)6![]()
【解析】
(1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,通过等量代换得到一对内错角相等;根据上步结论可推理得到平行线,再结合AE⊥ED即可证得结论;
(2)先判断△COD是等边三角形,根据等底同高的三角形的面积相等可知S△ACD=S△COD,从而∠CAD与弧CD围成的阴影部分的面积=扇形COD的面积.
解:(1)直线DE与⊙O相切,
理由如下:连接OD,如图所示:
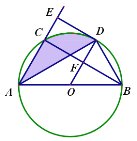
∵AD平分∠BAC,
∴∠EAD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠EAD,
∴EA∥OD,
∵DE⊥EA,
∴DE⊥OD,
又∵点D在⊙O上,
∴直线DE与⊙O相切;
(2)连接CD,OC.
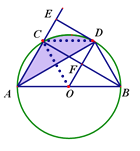
∵AD=BC,
∴ 弧AD =弧BC ,
∴ 弧AC = 弧BD ,
∵ 弧CD = 弧BD ,
∴ 弧AC = 弧CD =弧BD,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴∠CDO=∠DOB=60°,
∴CD∥AB,
∴S△ACD=S△COD,
∴∠CAD与弧CD围成的阴影部分的面积=扇形COD的面积=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目