题目内容
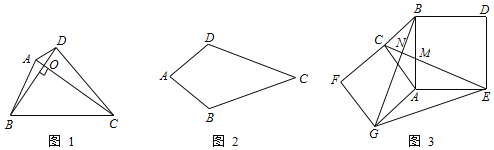
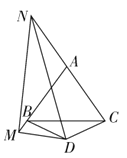
【题目】如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探BM,MN,CN之间的数量关系,并给出证明.
【答案】CN=MN+BM,见解析
【解析】
采用“截长补短”法,在CN上截取点E,使CE=BM,连接DE,结合等边及等腰三角形的性质利用SAS可证△MBD≌△ECD,继而可证△MND≌△END,由全等的性质可得结论.
解:CN=MN+BM.证明:
如图,在CN上截取点E,使CE=BM,连接DE,
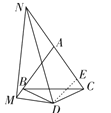
∵△ABC为等边三角形,
∴∠ACB=∠ABC=60°.
又∵△BDC为等腰三角形,且∠BDC=120°,
∴BD=CD,∠DBC=∠BCD=30°.
∴∠ABD=∠ABC+∠DBC=∠ACB+∠BCD=∠ECD=90°.
![]()
在△MBD和△ECD中,
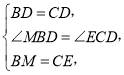
∴△MBD≌△ECD(SAS).
∴MD=ED,∠MDB=∠EDC.
又∵∠MDN=60°,∠BDC=120°,
∴∠EDN=∠BDC-(∠BDN+∠EDC)=∠BDC-(∠BDN+∠MDB)=∠BDC-∠MDN=120°-60°=60°.
∴∠MDN=∠EDN.
在△MND与△END中,
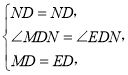
∴△MND≌△END(SAS).
∴MN=NE.
∴CN=NE+CE=MN+BM.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?