题目内容
【题目】已知:二次函数y=2x2+4x+m﹣1,与x轴的公共点为A,B. 
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点; ①当m=1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n<8时,结合函数的图象,求m的取值范围.
【答案】
(1)解:∵A与B重合,
∴二次函数y=2x2+4x+m﹣1的图象与x轴只有一个公共点,
∴方程2x2+4x+m﹣1=0有两个相等的实数根,
∴△=42﹣4×2(m﹣1)=24﹣8m=0,
解得:m=3.
∴如果A与B重合,m的值为3.
(2)解:①当m=1时,原二次函数为y=2x2+4x+m﹣1=2x2+4x,
令y=2x2+4x=0,则x1=0,x2=﹣2,
∴线段AB上的整点有(﹣2,0)、(﹣1,0)和(0,0).
故当m=1时,线段AB上整点的个数有3个.
②由点A,B之间的部分与线段AB所围成的区域内(包括边界)可用以下不等式表示
如图,
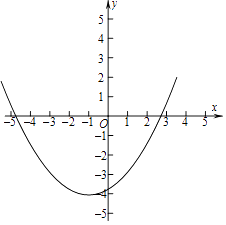
对于二次函数y=2x2+4x+m﹣1,可知对称轴x=﹣1,
∵抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,且1<n<8,
∴x=0时,y≤0;x=3时,y>0;
则有 ![]() ,
,
解得:﹣29<m≤1.
【解析】(1)当A、B重合时,抛物线与x轴只有一个交点,此时△=0,从可求出m的值.(2)①m=1代入抛物线解析式,然后求出该抛物线与x轴的两个交点的坐标,从而可求出线段AB上的整点;②根据二次函数表达式可以用带m表达出两根之差,根据1<两根之差<8,即可解题.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.