题目内容
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 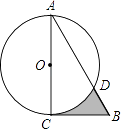
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
【答案】A
【解析】解:如图连接OD、CD. ∵AC是直径,
∴∠ADC=90°,
∵∠A=30°,
∴∠ACD=90°﹣∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵BC是切线.
∴∠ACB=90°,∵BC=2 ![]() ,
,
∴AB=4 ![]() ,AC=6,
,AC=6,
∴S阴=S△ABC﹣S△ACD﹣(S扇形OCD﹣S△OCD)
= ![]() ×6×2
×6×2 ![]() ﹣
﹣ ![]() ×3×3
×3×3 ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×32)
×32)
= ![]() ﹣
﹣ ![]() π.
π.
故选A.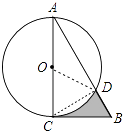
【考点精析】根据题目的已知条件,利用含30度角的直角三角形和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察这些统计数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式.
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)