题目内容
【题目】在甲、乙两个不透明的口袋中,分别有4个和3个大小、材质完全相同的小球,其中甲口袋中的小球上标有数字0,1,2,3,乙口袋中的小球上分别标有数字1,2,3,先从甲口袋中随机摸出一个小球,记下数字为![]() ,再从乙口袋中随机摸出一个小球,记下数字为
,再从乙口袋中随机摸出一个小球,记下数字为![]() .
.
(1)请用列表法或画树状图的方法表示出所有![]() 可能的结果;
可能的结果;
(2)规定:若![]() 都是方程
都是方程![]() 的解时,则小明获胜;若
的解时,则小明获胜;若![]() 都不是方程
都不是方程![]() 的解时,则小宇获胜,问他们两人谁获胜的概率大?
的解时,则小宇获胜,问他们两人谁获胜的概率大?
【答案】(1)树状图和12种结果见解析;(2)两人获胜的概率一样大
【解析】
(1)根据画树形图即可表示出所有可能出现的结果;
(2)分别求出两个人赢的概率,再进行判断即可.
(2)m,n都是方程![]() 的解的结果有2个,m,n都不是方程
的解的结果有2个,m,n都不是方程![]() 的解的结果有2个,然后根据概率公式分别求出两个人赢的概率,再进行判断即可.
的解的结果有2个,然后根据概率公式分别求出两个人赢的概率,再进行判断即可.
解:(1)画树状图如下:
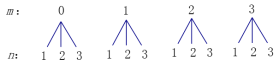
所有(m,n)可能的结果有(0,1),(0,2),(0,3),(1,1),(1,2),(1,3)
(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)
共12种结果
(2)由![]() 得x=1,或x=2
得x=1,或x=2
∴m,n都是方程![]() 的解时,结果数有(1,2),(2,1)两种
的解时,结果数有(1,2),(2,1)两种
∴小明获胜的概率![]()
m,n都不是方程![]() 的解时,结果数有(0,3),(3,0)两种
的解时,结果数有(0,3),(3,0)两种
∴小宇获胜的概率![]()
∴![]()
故两人获胜的概率一样大.

 名校课堂系列答案
名校课堂系列答案【题目】小明和小红为了更直观了解“物体质量”的概念,各选五个鸡蛋称重,以每个![]() 为标准,大于或等于
为标准,大于或等于![]() 即为达标,超过标准部分的克数记为正数,不足标准部分的克数记为负数.小明所统计的数据为实际称重读数,小红为记录数据,把所得数据整理成如下统计表(单位:
即为达标,超过标准部分的克数记为正数,不足标准部分的克数记为负数.小明所统计的数据为实际称重读数,小红为记录数据,把所得数据整理成如下统计表(单位:![]() ).
).
序号 数据 姓名 | 1 | 2 | 3 | 4 | 5 |
小明 | 48 | 50 |
| 49 | 51 |
小红 |
|
|
| 2 | 1 |
经过统计发现,小明所选鸡蛋质量的平均数为![]() ,小红所选鸡蛋质量的众数为
,小红所选鸡蛋质量的众数为![]() ,根据以上信息:
,根据以上信息:
(1)填空:![]() ,
,![]() ;
;
(2)通过计算说明,小明和小红哪个选取的鸡蛋大小更均匀,请说明理由;
(3)现从小明和小红所选取的鸡蛋里各随机挑一个,这两个鸡蛋质量都达标的概率是多少?
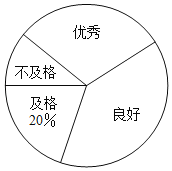
【题目】某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 | 频数(人) | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.