题目内容
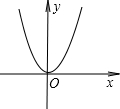 已知二次函数y=x2-2x-1.
已知二次函数y=x2-2x-1.(1)求此二次函数的图象与x轴的交点坐标;
(2)二次函数y=x2的图象如图所示,将y=x2的图象经过怎样的平移,就可以得到二次函数y=x2-2x-1的图象.(参考:二次函数y=ax2+bx+c图象的顶点坐标是(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
分析:(1)解方程x2-2x-1=0即可得出抛物线与x轴的交点的横坐标;
(2)先求得抛物线y=x2-2x-1的顶点坐标,然后就可以解答抛物线的平移问题.
(2)先求得抛物线y=x2-2x-1的顶点坐标,然后就可以解答抛物线的平移问题.
解答:解:(1)x2-2x-1=0解得x1=1+
,x2=1-
,
∴图象与x轴的交点坐标为(1+
,0)和(1-
,0).
(2)-
=-
=1,
=
=-2,
∴顶点坐标为(1,-2),
将二次函数y=x2图象向右平移1个单位,再向下平移2个单位,
就可得到二次函数y=x2-2x-1的图象.
| 2 |
| 2 |
∴图象与x轴的交点坐标为(1+
| 2 |
| 2 |
(2)-
| b |
| 2a |
| -2 |
| 2×1 |
| 4ac-b2 |
| 4a |
| -4×1-(-2)2 |
| 4×1 |
∴顶点坐标为(1,-2),
将二次函数y=x2图象向右平移1个单位,再向下平移2个单位,
就可得到二次函数y=x2-2x-1的图象.
点评:抛物线平移问题,实际上就是两条抛物线顶点之间的问题,找到了顶点的变化就知道了抛物线的变化.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
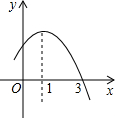 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).