题目内容
【题目】如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数. 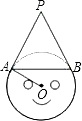
【答案】解:方法一:∵PA、PB切⊙O于A、B, ∴PA=PB,
∴OA⊥PA,
∵∠OAB=25°,
∴∠PAB=65,
∴∠APB=180﹣65°×2=50°;
方法二:连接OB,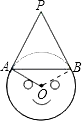
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OP⊥AB,
∴∠OAP+∠OBP=180°,
∴∠APB+∠AOB=180°;
∵OA=OB,
∴∠OAB=∠OBA=25°,
∴∠AOB=130°,
∴∠APB=50°;
方法三:连接OP交AB于C,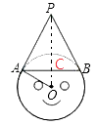
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OP⊥AB,
OP平分∠APB,
∴∠APC=∠OAB=25°,
∴∠APB=50°.
【解析】连OB,OP,由AO=OB得,∠OAB=∠OBA=25°,∠AOB=180°﹣2∠BAB=130°;因为PA、PB分别相切于点A、B,则∠OAP=∠OBP=90°,所以∠APB=180°﹣∠AOB=50°.
【考点精析】根据题目的已知条件,利用切线的性质定理的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目