题目内容
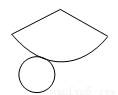
某物体的展开图如图所示,它的左视图为
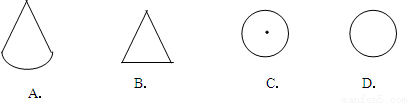
B.
【解析】
试题分析:由物体的展开图的特征知,它是圆锥的平面展开图,又圆锥的左视图是三角形.
故选B.
考点:几何体的展开图.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
某物体的展开图如图所示,它的左视图为

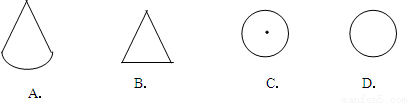
B.
【解析】
试题分析:由物体的展开图的特征知,它是圆锥的平面展开图,又圆锥的左视图是三角形.
故选B.
考点:几何体的展开图.

 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案