ΧβΡΩΡΎ»ί
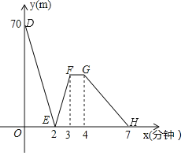
ΓΨΧβΡΩΓΩ”–“ΜΩΤΦΦ–ΓΉιΫχ––ΝΥΜζΤς»Υ––ΉΏ–‘Ρή ‘―ιΘ§‘Ύ ‘―ι≥ΓΒΊ”–AΓΔBΓΔC»ΐΒψΥ≥¥Έ‘ΎΆ§“Μ± ÷±ΒΡ»ϋΒά…œΘ§ΦΉΓΔ““ΝΫΜζΤς»ΥΖ÷±π¥”AΓΔBΝΫΒψΆ§ ±Ά§œρ≥ωΖΔΘ§Ψ≠Ιΐ7minΆ§ ±ΒΫ¥οCΒψΘ§““ΜζΤς»Υ Φ÷’“‘60m/minΒΡΥΌΕ»––ΉΏΘ§»γΆΦ «ΦΉΓΔ““ΝΫΜζΤς»Υ÷°ΦδΒΡΨύάκyΘ®mΘ©”κΥϊΟ«ΒΡ––ΉΏ ±ΦδxΘ®minΘ©÷°ΦδΒΡΆΦœσΘ§«κΫαΚœΆΦœσΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©AΓΔBΝΫΒψ÷°ΦδΒΡΨύάκ «ΓΓ ΓΓmΘ§ΦΉΜζΤς»Υ«Α2minΒΡΥΌΕ»ΈΣΓΓ ΓΓm/minΘ°
Θ®2Θ©»τ«Α3minΦΉΜζΤς»ΥΒΡΥΌΕ»≤Μ±δΘ§«σ≥ω«Α3minΘ§ΦΉΓΔ““ΝΫΜζΤς»Υ÷°ΦδΒΡΨύάκyΘ®mΘ©”κΥϊΟ«ΒΡ––ΉΏ ±ΦδrΘ®minΘ©÷°ΦδΒΡΙΊœΒ ΫΘ°
Θ®3Θ©«σ≥ωΝΫΜζΤς»Υ≥ωΖΔΕύ≥Λ ±ΦδœύΨύ28mΘ°
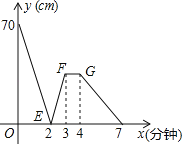
ΓΨ¥πΑΗΓΩΘ®1Θ©70Θ§95ΘΜΘ®2Θ©yΘΫ35r©¹70ΘΜΘ®3Θ©ΝΫΜζΤς»Υ≥ωΖΔ1.2Μρ2.8Μρ4.6min ±œύΨύ28m
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΆΦœσΫαΚœΧβ“βΘ§Φ¥Ω…ΒΟ≥ωAΓΔBΝΫΒψ÷°ΦδΒΡΨύάκ «70mΘ°…ηΦΉΜζΤς»Υ«Α2minΒΡΥΌΕ»ΈΣxm/minΘ§ΗυΨί2Ζ÷÷”ΦΉΉΖ…œ““Ν–≥ωΖΫ≥ΧΘ§Φ¥Ω…«σΫβΘΜ
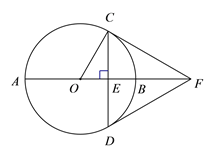
Θ®2Θ©œ»«σ≥ωFΒψΒΡΉχ±ξΘ§‘Ό…ηœΏΕΈEFΥυ‘Ύ÷±œΏΒΡΚ· ΐΫβΈω ΫΈΣyΘΫkr+bΘ§ΫΪEΓΔFΝΫΒψΒΡΉχ±ξ¥ζ»κΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…«σΫβΘΜ
Θ®3Θ©…η![]() Θ§ΗυΨίΆΦœσΩ…÷ΣΝΫΜζΤς»ΥœύΨύ28m ±”–»ΐΗω ±ΩΧ(0ΓΪ2Θ§2ΓΪ3Θ§4ΓΪ7)Ζ÷±π«σ≥ωDEΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΓΔGHΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΘ§‘ΌΝνyΘΫ28Θ§Ν–≥ωΖΫ≥Χ«σΫβΦ¥Ω…Θ°
Θ§ΗυΨίΆΦœσΩ…÷ΣΝΫΜζΤς»ΥœύΨύ28m ±”–»ΐΗω ±ΩΧ(0ΓΪ2Θ§2ΓΪ3Θ§4ΓΪ7)Ζ÷±π«σ≥ωDEΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΓΔGHΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΘ§‘ΌΝνyΘΫ28Θ§Ν–≥ωΖΫ≥Χ«σΫβΦ¥Ω…Θ°
Θ®1Θ©”…Χβ“βΘ§Ω…ΒΟAΓΔBΝΫΒψ÷°ΦδΒΡΨύάκ «70mΘ°
…ηΦΉΜζΤς»Υ«Α2minΒΡΥΌΕ»ΈΣxm/minΘ§
ΗυΨίΧβ“βΘ§ΒΟ![]() Θ§ΫβΒΟxΘΫ95Θ°
Θ§ΫβΒΟxΘΫ95Θ°
Ι ¥πΑΗΈΣ70Θ§95ΘΜ
Θ®2Θ©»τ«Α3minΦΉΜζΤς»ΥΒΡΥΌΕ»≤Μ±δΘ§”…Θ®1Θ©Ω…÷ΣΘ§«Α3minΦΉΜζΤς»ΥΒΡΥΌΕ»ΈΣ95m/minΘ§
‘ρFΒψΉίΉχ±ξΈΣΘΚ![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°
…ηœΏΕΈEFΥυ‘Ύ÷±œΏΒΡΚ· ΐΫβΈω ΫΈΣ![]() Θ§
Θ§
ΫΪ![]() ¥ζ»κΘ§
¥ζ»κΘ§
![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
‘ρœΏΕΈEFΥυ‘Ύ÷±œΏΒΡΚ· ΐΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΘ§…η![]() Θ°
Θ°
ΓΏ![]() Θ§
Θ§
ΓύœΏΕΈDEΥυ‘Ύ÷±œΏΒΡΚ· ΐΫβΈω ΫΈΣ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύœΏΕΈGHΥυ‘Ύ÷±œΏΒΡΚ· ΐΫβΈω ΫΈΣ![]() Θ§
Θ§
…ηΝΫΜζΤς»Υ≥ωΖΔtmin ±œύΨύ28mΘ§
”…Χβ“βΘ§Ω…ΒΟ![]() Θ§Μρ
Θ§Μρ![]() Θ§Μρ
Θ§Μρ![]() Θ§
Θ§
ΫβΒΟtΘΫ1.2Θ§ΜρtΘΫ2.8Θ§ΜρtΘΫ4.6Θ§
Φ¥ΝΫΜζΤς»Υ≥ωΖΔ1.2Μρ2.8Μρ4.6min ±œύΨύ28mΘ°