Question

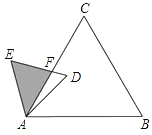
【题目】如图，在△ABC中，∠ABC=∠ACB。

（1）若D为BC边上一点，E为直线AC上一点，且∠ADE=∠AED.求证：∠BAD=2∠CDE；

（2）如图，若D在BC的反向延长线上，其它条件不变，（1）中的结论是否仍然成立？证明你的结论.

Answer 1

【答案】（1）见解析；（2）（1）中的结论仍然成立，见解析.

【解析】

（1）由三角形外角的性质可得∠AED＝∠ACB＋∠CDE，∠ADC＝∠ADE＋∠CDE＝∠BAD＋∠ABC，再根据∠ADE＝∠AED，∠ABC＝∠ACB即可证明；

（2）与（1）中推理方法类似，证明即可.

解：（1）证明：如图1，

∵∠AED是△CDE的外角

∴∠AED＝∠ACB＋∠CDE，

∵∠ADC是△ABD的外角

∴∠ADC＝∠ADE＋∠CDE＝∠BAD＋∠ABC，

∵∠ADE＝∠AED

∴∠ACB＋∠CDE＋∠CDE＝∠BAD＋∠ABC，

∵∠ABC＝∠ACB，

∴∠BAD＝2∠CDE；

（2）（1）中的结论仍然成立，理由如下：

如图2，∵∠ACB是△CDE的外角

∴∠ACB＝∠AED＋∠CDE，

∵∠ABC是△ABD的外角

∴∠ABC＝∠ADB＋∠BAD，

∵∠ABC＝∠ACB，

∴∠AED＋∠CDE＝∠ADB＋∠BAD，

∵∠AED＝∠ADE＝∠CDE＋∠ADB

∴∠CDE＋∠ADB＋∠CDE＝∠ADB＋∠BAD

∴∠BAD＝2∠CDE．