题目内容
如图所示,已知等腰直角三角形ABC的腰长为acm,矩形DEFG的相邻两边分别与这个三角形的腰和斜边相等,如果将这两个图形组合成一个图形(要求有一条边重合,并且除此之外,再无公共部分).(1)请分别画出各种不同的组合方式(可画示意图).
(2)△ABC的直角顶点A到矩形各顶点的距离中,共有几种不同的距离?哪种组合中的哪个距离最长,为什么?
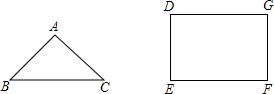
分析:(1)由题意得,矩形DEFG的相邻两边分别与这个三角形的腰和斜边相等,即AB=AC=DE=GF,BC=DG=EF,可使相等的线段重合即可;(2)计算两种图形中到到矩形各顶点的距离,共有四种不同的距离,比较得出结果.
解答:解:(1)
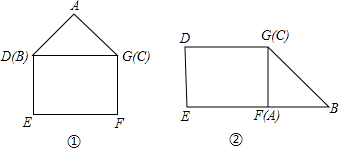
(2)共有四种不同的距离:
①AD=a(图①中);
②AE=
=
•a(图①中);
③EF=
a(图②中);
④FD=
=
•a(图②中).
∵
>
>
>1,
∴①中AE的距离最长,为
a.

(2)共有四种不同的距离:
①AD=a(图①中);
②AE=
(
|
2+
|
③EF=
| 2 |
④FD=
a2+(
|
| 3 |
∵
2+
|
| 3 |
| 2 |
∴①中AE的距离最长,为
2+
|
点评:此题主要考查等腰三角形下、矩形的性质,综合利用勾股定理.

练习册系列答案
相关题目
 如图所示,已知等腰三角形ABC,AB边的垂直平分线交AC于点D,交AB于E,AB=AC=8,BC=6,求△BDC的周长.
如图所示,已知等腰三角形ABC,AB边的垂直平分线交AC于点D,交AB于E,AB=AC=8,BC=6,求△BDC的周长.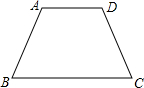 如图所示,已知等腰梯形ABCD中,AD∥BC,下底BC与上底AD的差恰好等于腰长AB,则∠BAD=( )
如图所示,已知等腰梯形ABCD中,AD∥BC,下底BC与上底AD的差恰好等于腰长AB,则∠BAD=( )